Here’s a problem on averages that has been used by many teachers over the years. I like the additional ‘sting in the tail’ as it really makes pupils think about real life and it is an instant use of calculating the mean from an ungrouped frequency table.

Image Credit: www.vivcorecruitment.co.uk
The Problem
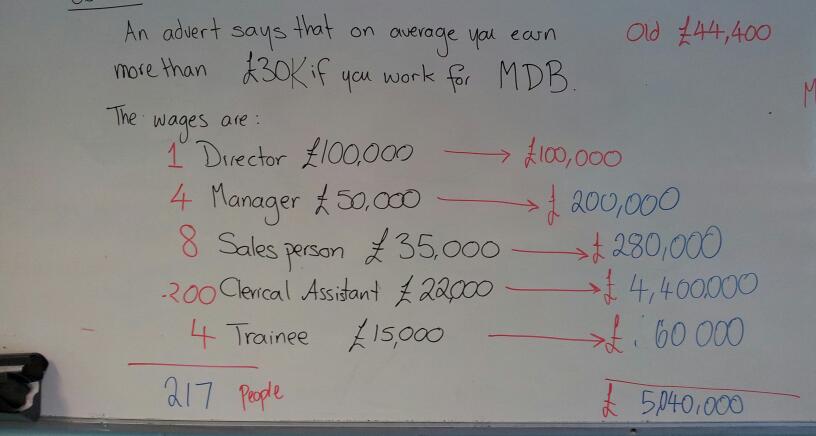
A job advert says that the average worker at OfficesRUs earns over £30 thousand pounds.
OfficesRUs Salaries:
- Director £100,000
- Manager £50,000
- Sales Person £35,000
- Clerical Assistant £22,000
- Trainees £15,000
Is the advert true?
The Discussion
If pupils calculate the mean they will find it is £44,400 – this makes the advert true
But why would a company have the same number of employees at each pay grade?
The Sting
OfficesRUs is a clerical agency, offering temporary clerical staff for other businesses. Their staff numbers are:
- 1 Director £100,000
- 4 Managers £50,000
- 8 Sales People £35,000
- 200 Clerical Assistants £22,000
- 4 Trainees £15,000
Is the advert still true?
The Result
My class worked out how much each pay grade would get and added them to find the total salary cost. Some pupils then divided by 5, but discovered that the mean would be far greater than the Director’s salary. They then realised they had to total up the employees too. The mean turned out to be less than £30,000. This then leads to a discussion of which measure of average is best in this situation.
This is the working out from my board. The original problem is in black, with the sting and working in red. We linked the individual pay grade calculations to the work we had done on means from ungrouped frequency tables. The layout of the calculations is very similar to our tables.
This was a really good investigative starter to bridge between a theory and problem solving lesson. You could get pupils to see if they can find any examples of job adverts with average salaries in and make up their own problems.