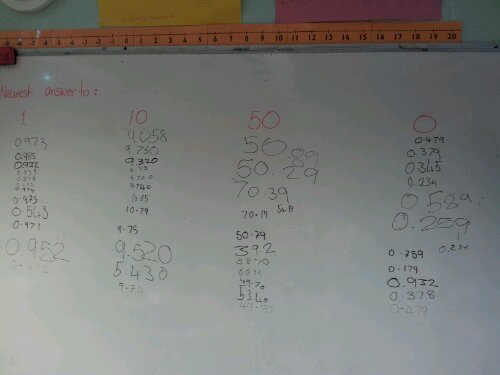
This weekend I was at TeachMeet NorthWest at Calderstones School in Liverpool. A TeachMeet is a free event where anyone can present so long as it’s relevant to education and only lasts 5 minutes.
It was the first TM I’ve been to and I also presented. I’m not sure if anyone understood the opening line of ‘S’mae, dw i’n hoffi deinosoriaid’ (Hi, I like dinosaurs) but at least I did my best for languages day as a Maths ASTosaurus*.
Reflecting on the whole event, I can safely say that it was the most energising CPD event I’ve ever attended. You could never run such a diverse event as a fee paying course. The element of the unknown, not knowing what the next topic would be, kept everyone engaged. The pace didn’t let up – there was no time to get bored or doodle on handouts. By the time I got home, my colleague J and myself had already discussed half a dozen ideas we would implement and come up with a Departmental project that would be good for both our Performance Management and whole school BLP focus.
So, I’m taking a week out of blogging to try out all these amazing ideas that are buzzing around my head. Then I’ll share who the brains are behind the ideas (so you can follow them on Twitter) and the impact they’ve had.
* I describe myself as an ASTosaurus as the AST grade was abolished nationally this year. There are still ASTs, but most are being moved to Lead Practitioner roles.
For those who don’t know, an AST is an Advanced Skills Teacher. To become one, you must prove yourself to be outstanding in all areas and pass an assessment. Unlike Excellent teachers and Lead Practitioners, ASTs can only be assessed by an assessment body from London. Less than 5% of teachers are ASTs and now we are going the way of the dinosaurs.