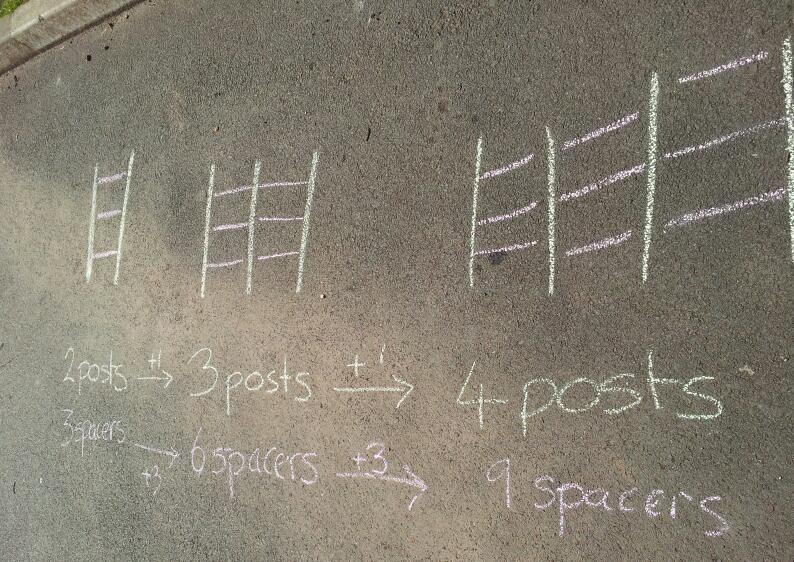So I’m all ready to teach a lesson recapping number patterns from the basics for a lower ability group … then a visitor to the Department arrives and asks if it’s okay if they observe my lesson. They’ve been told that there is usually something ‘off the wall’ happening in my room. Thanks … I think!
Well, I’m not one to disappoint. A little fun with the starter perhaps? The sun is shining and I’ve got whiteboards and chalk …
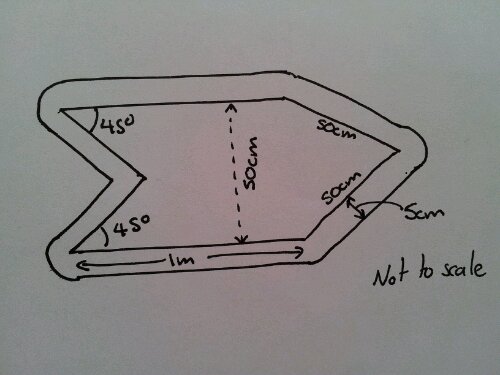
We’ve all seen fence panel number patterns. Here is a fence:

What can you see?
We discussed the pattern linking number of posts and spacers. We then represented the fence in colour coded symbols (yes, we have chalk in more than one colour!) and annotated it.
The class were then sent off to find their own patterns. They found repeating patterns and made notes on their whiteboards. Once they were happy with their work they could chalk it out.
This group looked at number of slats on a bench with number of benches.

They represented each bench as an ‘L’ and each slat with an ‘o’.
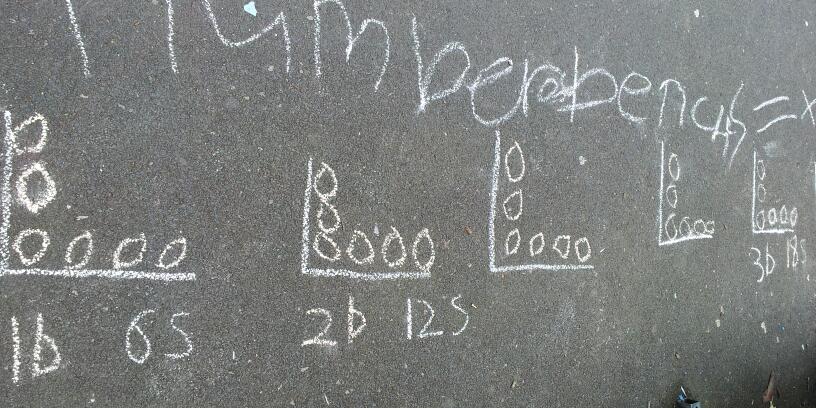
They worked out:
No of benches x 6 = No of slats
Other groups looked at number of windows & number of classrooms and number of benches & number of picnic tables.
We then went back to our quiet number pattern work in the classroom.
This task is easily adaptable for many aspects of number, including ratio and proportion.