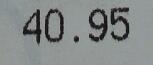Tag Archives: range

308. Zombie stats

Leave a reply

I’ve used word length analysis for years as a source of comparative statistics. The concept is easy – you take a children’s book and a grown up book and compare the word lengths of the first 20, 40, 80 words. After you collect the information in a table, you can use this data to compare averages and the range.

Image credit: www.comingsoon.net
But what texts to use? Well – you can’t beat a bit of Dr Seuss, but what grown up text could you use. I can highly recommend this extract from ‘Pride and Prejudice and Zombies’:

Pride and Prejudice and Zombies by Seth Grahame Smith

Not only will you be investigating mathematical concepts, but you might just be inspiring a student to pick up a book and read.
Update: If you use the first chapter (say thirty words) of ‘Pride & Prejudice & Zombies’ you get some interesting data. The range is wide, but the highest frequency word length is just two. It’s a great conversation piece – why does this happen? The language is a very precise parody of 19th prose with all the correct connectives and no contractions eg ‘it is’ not ‘it’s’.

247. The Elf Challenge

Leave a reply

It was the month before Christmas and all through the house not a creature was stirring – except for the senior elves who were on the brink of all out war. Father Christmas had picked up some leadership strategies on his travels and decided to send his management elves on a team building day … paintballing!

Don’t be fooled – this is no simple Christmas time-filler. This task requires problem solving strategies, two-way tables, averages, data analysis and logic. In fact, you might want to have a go yourself. There is a task sheet, support sheet and solution.

The Elf Challenge (pdf)

Enjoy the puzzled faces and watch the arguments when students try to justify their answers.

197. £40.95

Leave a reply

Today we have a discussion starter question for you, inspired by a trip to the shops.

image

My shopping cost £40.95 today. What is the smallest number of coins required to make this amount?
If I paid with two £20s and a £10 note, what is the most efficient change?
Why would someone pay £41.05, as opposed to £41?

I purchased 17 items, do you have enough information to calculate the mean?
The most expensive item was £10, the cheapest was 45p. What does this allow you to calculate?
Two luxury items cost £9 in total. If I hadn’t bought these, what would the mean have been? Does this effect the range?

When I paid I was given this voucher:

image

What would the shopping have cost somewhere else?
What would the mean cost per item be after this discount?
What percentage discount is this?

You could also use this as a discussion starter about the number skills you use when you go shopping.

113. Did the Little Thinkers get you thinking?

1 Reply

Did my Little Thinkers give you ideas for a lesson?

I hope so!

These are my little crisp people and they’ve been helping pupils learn for over a decade.

I first thought up this task when an interactive whiteboard and digital projector came in the form of an overhead projector. Using the brand new concept of colour printing onto inkjet OHP transparencies, we could move these little people around the board and investigate different problems. Each number represents the number of bags of crisps eaten in a week. Each colour represents a flavour (Blue = salt & vinegar, red = ready salted, green = cheese & onion, pink = prawn cocktail).

You can sort by number of bags eaten:

image

You can create a flavour pictogram:

image

In fact you can use this resource with KS2 & KS3 to investigate lots of topics:
Sorting by category (number/colour)
Ordering numbers
Pictograms
Venn diagrams
Carroll diagrams
Bar-charts
Averages
Questionning
Probability

And anything else you can think of.

I’ve created an editable template of figures, in three different sizes. You print them out and use them individually, in group work or on the wall. There is also a teacher guide on how to use the crisp people.

Enjoy!

Download your little people below:

Editable template  crisp-people-template-blank

Teacher guide and presentation crisp_people_guide

3. Class Averages

Leave a reply

This is my favourite activity for introducing different measures of average. You can do this in a corridor or outside, no special equipment required.

Set Up
Line up the class in height order

Range
Ask the shortest and tallest students to stand back to back. The difference in height is the range.

Median
Tell the first and last student to make a half turn. Ask the second and second to last student to make a half turn. Repeat until only one or two students are facing forward.
One pupil = median height.
Two pupils = halfway between their heights is the median.

Mean
Imagine everyone is the same height. Tell the students to try to be the same height by bending knees or standing on tiptoes. Explain the mean is about sharing out equally.

Mode
Ask students to put themselves into groups of the same height. The biggest group is the mode.

This activity links a numerical calculation with a physical activity, which makes it more memorable.