We recently finished teaching the AS Maths syllabus to Year 12. My colleague and I decided how to split up the start of the second year of the course. I’m starting with the modulus function.
I took one look at the skills needed at thought “Uh-oh”. The students are going to be out of practice with this. They are a lovely group, with a wide range of ability, but we’ve been very focussed on Applied Maths recently.
Option A: Go for it and patch up the vocabulary as we go (getting very frustrated – they knew this last October)
Option B: Break them in gently, recap the skills and vocabulary and extend them further
Option C: Reteach the work from last October.
Yes, you guessed it. I went with Option C. I found a brilliant task on piecewise function graphs on the Underground Maths website.
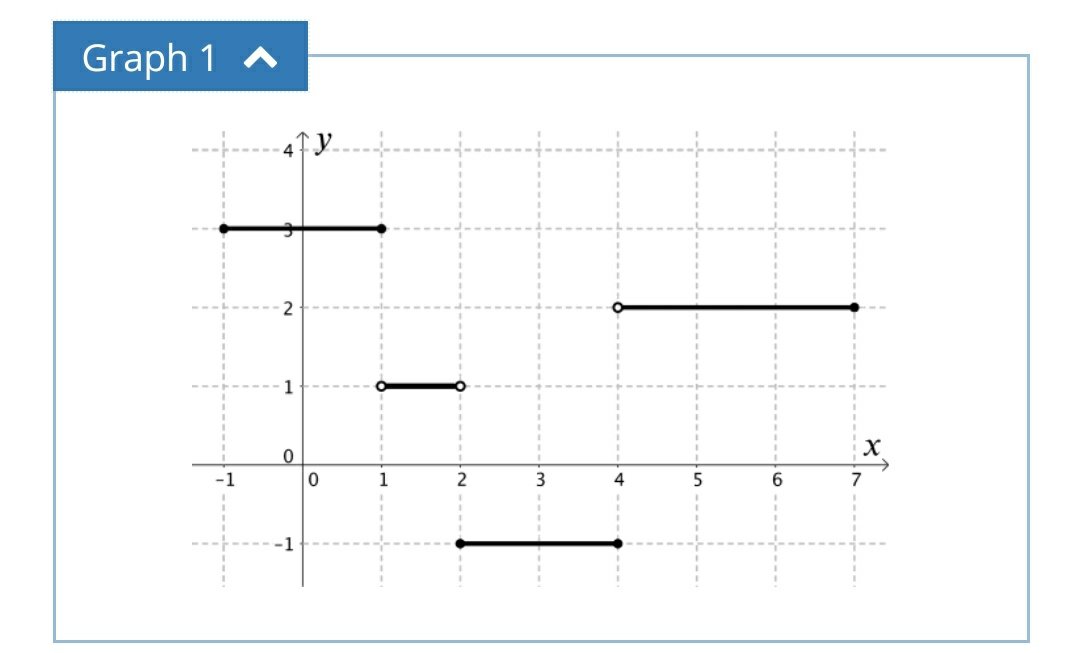
Image credit: https://undergroundmathematics.org/
There are four graphs given. The basic task is to interpret the functions relating to each graph, through description or function.
I photocopied the graphs onto card and sliced them up. Each group had a set of cards. One person described a graph and the others had to accurately draw it. Some students went straight onto squared paper, others drafted it out on mini whiteboards. They repeated this until all the graphs were drawn and everyone had had a go at describing (the describer stuck in their card, so that they had a complete set). Whilst they were doing this, I moved around and encouraged the use of mathematical vocabulary.
Note: it was interesting to see how many students had forgotten the significance of open and shaded circles to denote boundaries of inequalities.
The second task was to match up the function cards with the graphs. Once again, accuracy was key as not all graphs had functions and not all functions had graphs. There were also some that nearly, but not quite matched. This activity really brought out the key skills relating to domain, range and function notation that I was looking for. The extension task was to complete the missing pairs.
But, did it work? I can confirm that the following lesson the class made very good progress investing the modulus function and it’s graph, even going as far to solve equations. They knew what the notation meant, how to plot it and how to interpret the graphs.
I really like the Underground Maths website as it has great resources, good support material and always makes students think. Most of the time it gets teachers thinking too!
Like this:
Like Loading...