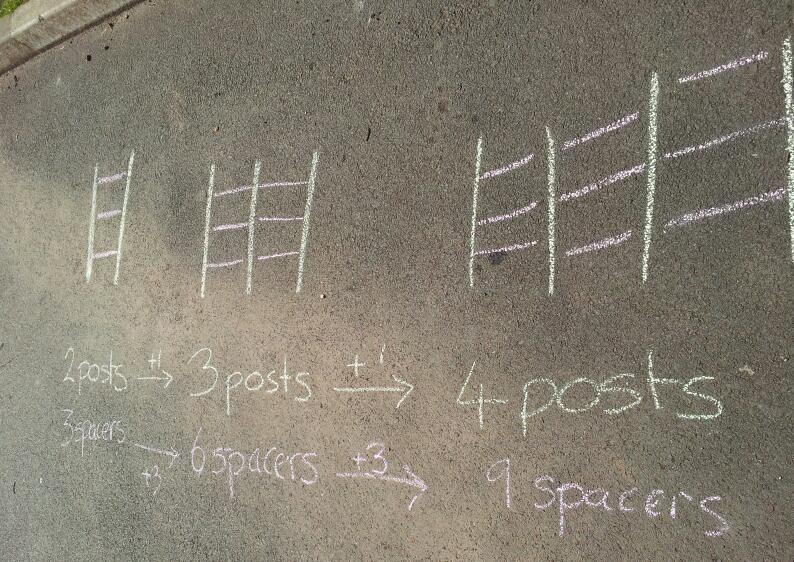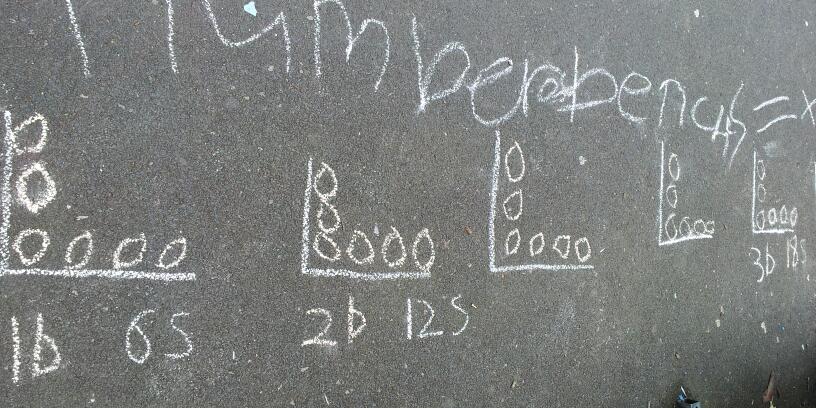Now what have a pair of roller skates got to do with number sequences? If you can guess before the reason, I’ll be surprised – it’ll mean there is more than one person as random as me!
Image Credit: No Fear adjustable quad skates/Amazon.co.uk
As you may have guessed from my earlier post 317. Pyramid Power I’m currently doing an Algebra unit on Number Sequences. I’ve changed the way I’ve taught this topic this year to incorporate a ‘Big Picture’ view as opposed to one lesson on drawing the next picture, the next on finding the Term to Term rule and finishing with a lesson on finding the Nth term. The beauty of mathematics lies in the connections we make, not the disparate skills.
After the investigative approach of the Pyramid Numbers lesson, we did some text book work on generating number sequences (eg Start with 5, add 3) expanding to look at the physical patterns each time, so the previous rule would have looked like N groups of 3 dots plus 2 dots. As with any class (mixed ability or not) there were varying levels of progression in these lessons. To pull everyone forward I wrote structured worksheets and allowed the students to choose which they did. I described them using the following comparisons with the roller disco at our local Sports Centre:
- Sheet 1 – beginner on roller skates, need a bit of hand holding (I’ll own up to demonstrating our local instructor’s technique for teaching beginners in front of the class)
- Sheet 2 – okay on skates, just a word of encouragement every now and then
- Sheet 3 – speedskating, no fear of the next challenge
- Extension – all the skills! Some tasty questions from a tough textbook exercise
After a student completes a sheet they just move to the next – there are no duplicate questions. I printed them A5 to stick neatly in their books but you might prefer A4. Solutions are provided.
Patterns and sequences A4 one per page
Patterns and sequences A4 two per page
Patterns and sequences solutions (docx)
Patterns and sequences solutions (pdf)
BTW I can tell you from personal experience that landing on your rear whilst speed skating really does hurt!