If you taught in England while mathematical coursework still existed, this post may not be new to you. However those who did not may be pleasantly surprised by the simple complexity of ‘Squashed Tomatoes’!
Aim
To investigate a growth pattern, which follows a simple rule.
Equipment
- Squared paper
- Coloured pens/pencils
- Ruler & pencil
Rules
Imagine a warehouse full of crates of tomatoes. One crate in the middle goes rotten. After an hour it infects the neighbouring crates which share one whole crate side. This second generation of rot infects all boxes which share exactly one side. Once a box is rotten it can only infect for an hour, then ceases to affect others. This sounds complicated, but trust me … it’s simple!
Picture Rules
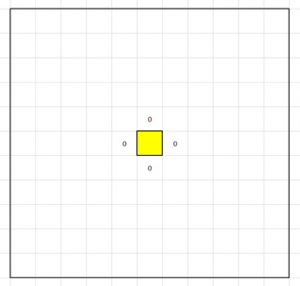
The first box goes rotten – colour in one square to represent the crate. The noughts represent the squares it will infect.
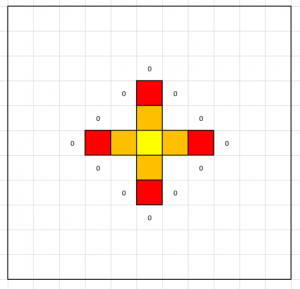
The second set of crates becomes rotten – use a different colour. The noughts represent what will become rotten next:
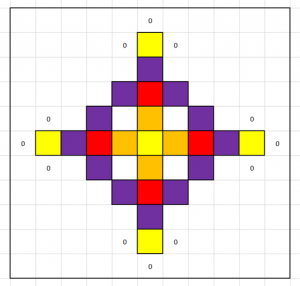
The third set of crates becomes rotten – change colour again. At this point it is useful to tell students to keep track of how many crates go rotten after each hour and how many are rotten in total:
The fourth set of crates forms a square:
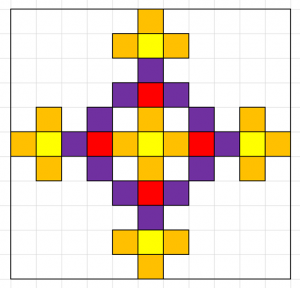
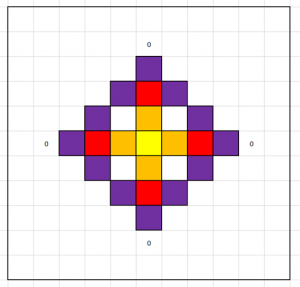 The fifth hour returns the pattern to adding one to each corner:
The fifth hour returns the pattern to adding one to each corner:
The sixth hour adds three onto each corner:
Now you can continue this pattern on for as big as your paper is. Students can investigate the rate of growth of rot or the pattern of rot per hour. As the pattern grows, the counting can get tricky. This is when my students started spotting shortcuts. They counted how many new squares were added onto each ‘arm’ and multiplied by number of ‘arms’.
Here are some examples of my students work:
This is a lovely part-completed diagram:

This piece of work includes a table of calculations – you can see the pattern of 1s, 4s and multiples of 12.

This is just amazing – you can see that alternate squares are coloured (except for the centre arms).

On this large scale you can see the fractal nature of this investigation.
Extension: Does this work for other types of paper? Isometric? Hexagonal?