This is a quick post on how I teach metric unit conversion for area and volume. All you need is a big whiteboard and coloured board pens.
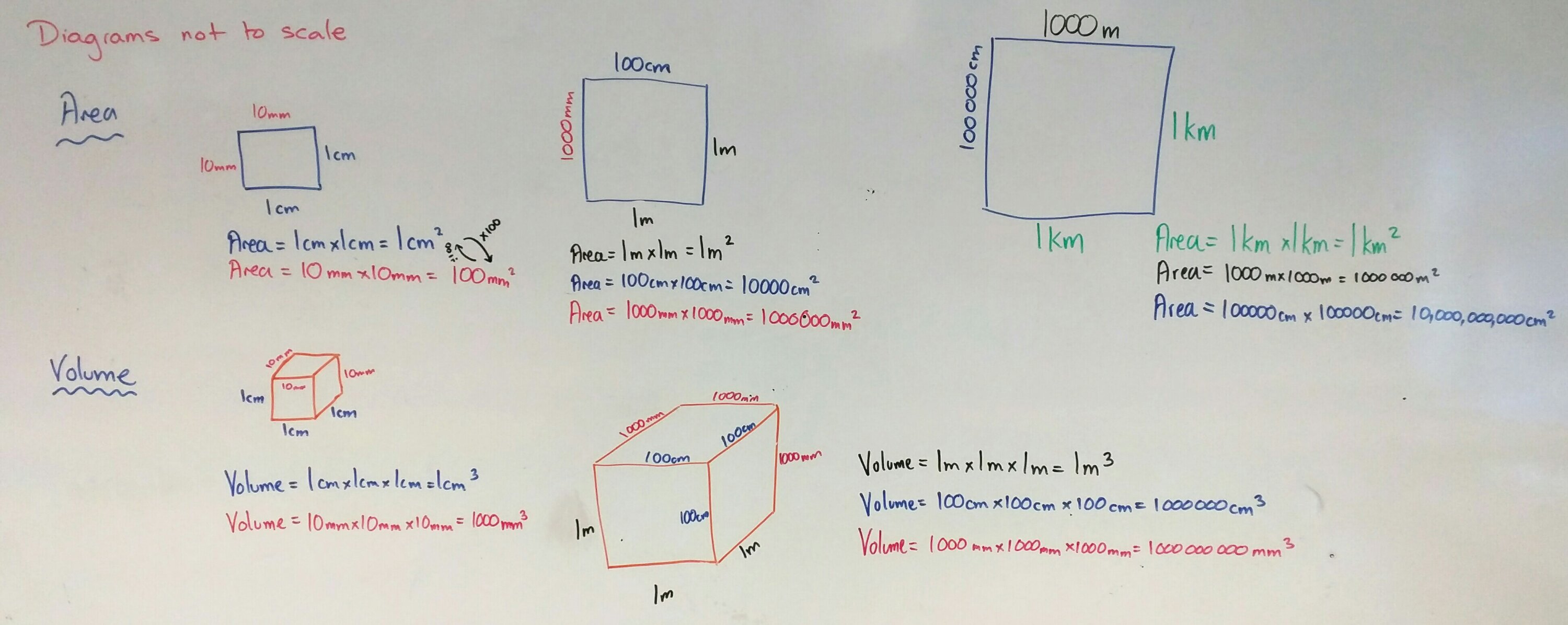
Start by stressing that all diagrams are not to scale/accurate.
Two colours
- Draw a square on the board
- Pen colour 1: Label it as 1cm
- What is the area? Show the calculation
- What is 1cm in mm?
- Pen colour 2: Label it as 10mm
- What is the area in mm? Show the calculation
- What is the scale factor between the sides? the area? why?
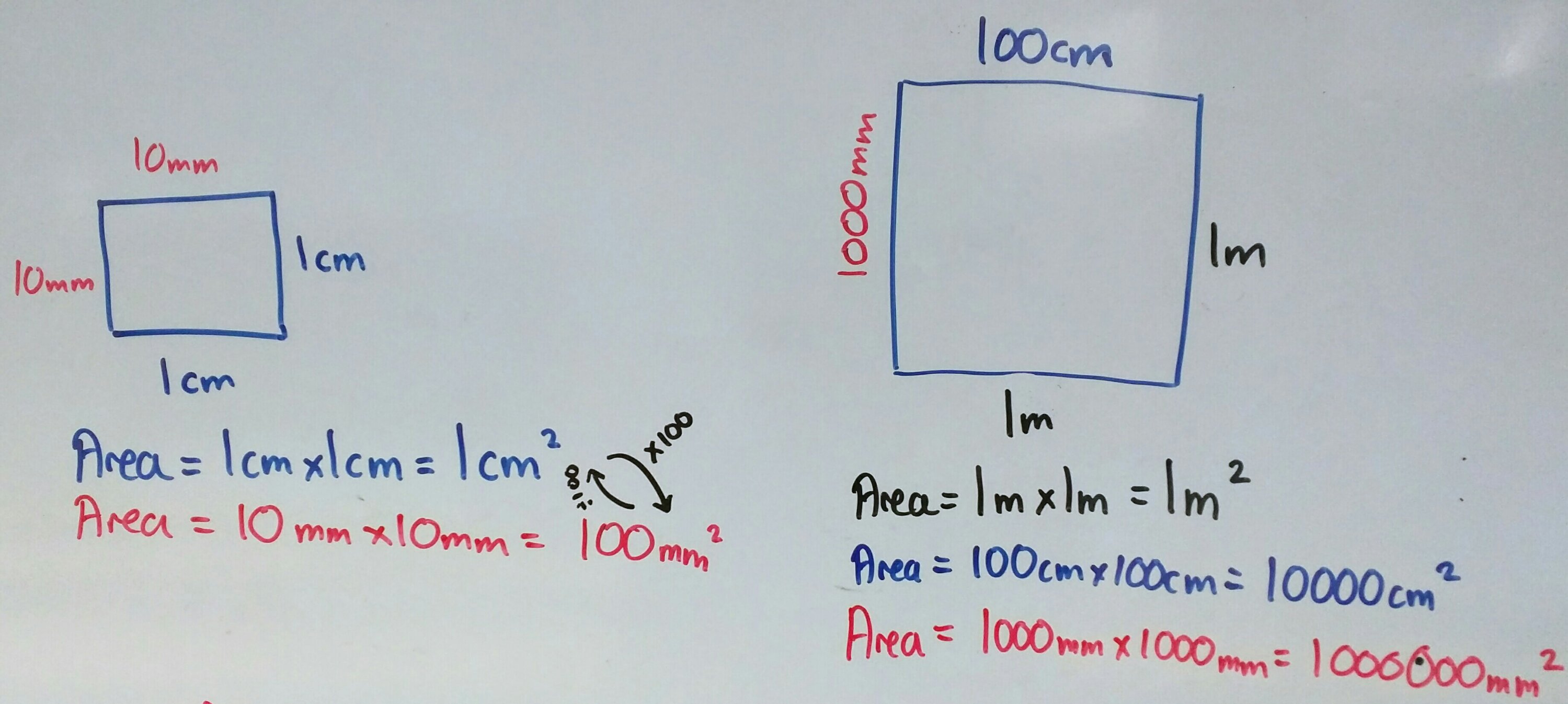
Three colours
- Draw a square on the board
- Pen colour 3: Label it as 1m
- What is the area? Show the calculation
- What is 1m in cm?
- Pen colour 2: Label it as 100cm
- What is the area in cm? Show the calculation
- What is the scale factor between the sides? the area? why?
- Repeat in pen colour 1 for mm
Four colours
Well not actually four colours – pens 2,3 & 4 only. Repeat the process for kilometres to metres and centimetres.
Volume – same process, just three dimensions
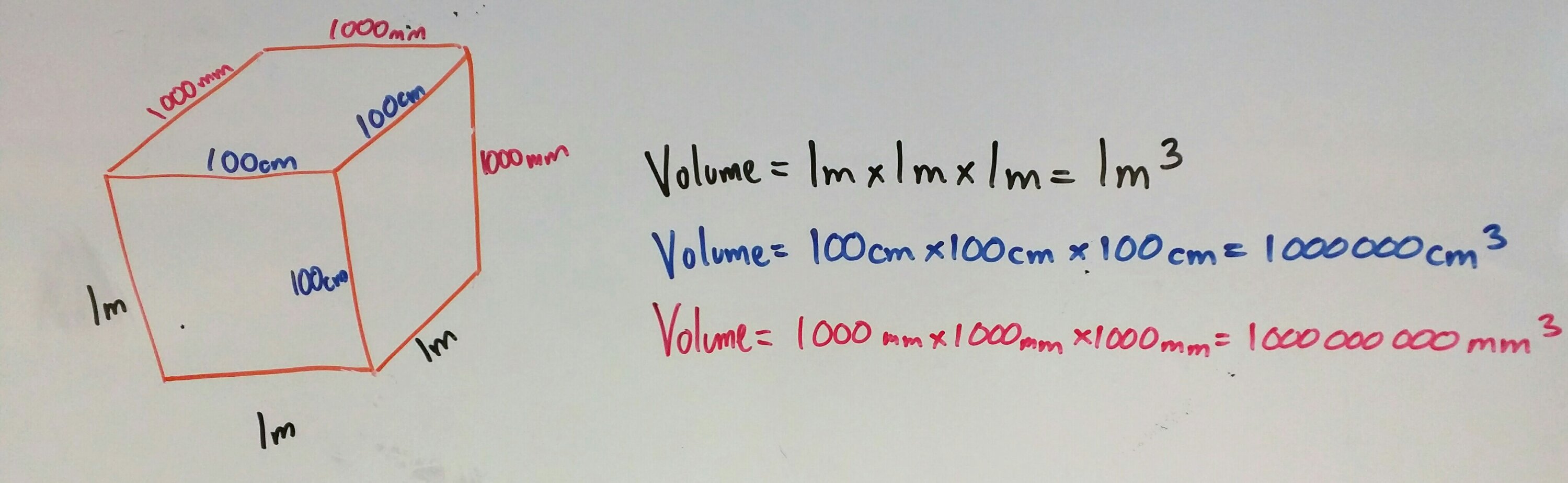
Why all the colours?
By coding each unit of measurement with a colour students can see the progression of the calculations and the links between area/volume and scale factor. After all, an okay mathematician can reproduce memorised facts, but a great mathematician doesn’t need to memorise – they understand where the calculations came from.
