You know that point when you’ve covered the Integration content in A2, the class can do all the different forms and then you set mixed questions … it’s like it’s in a different language. All that wonderful knowledge seeps out like water in a sieve. There must be a help sheet or tool that gives students a starting point, until their confidence and experience grows?
Rewind to proving an integration rule. I was discussing a textbook proof of an integration rule with a student and I just didn’t like it. It niggled in my head that I’d been shown a better method when I was first learning this stuff. After a quick dash to the stockroom and a climb up a step ladder, I found a later edition of the textbook I’d used at A-Level. I was right – the Bostock & Chandler proof was far more elegant and comprehensible. Problem solved!
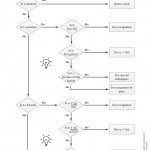
While I had this book out I had a flick through the pages. A flowchart caught my eye – not a fancy infographic, a proper ‘get the flowchart stencil out’ chart. It basically talks students through how to choose an integration strategy. I could have photocopied the page, but it was rubbish quality when I tried. I believe the book is now out of print, so I have recreated the flowchart page with full credit to it’s source. I hope it helps your students as much as it has mine.
C4 Integration flowchart (pdf)