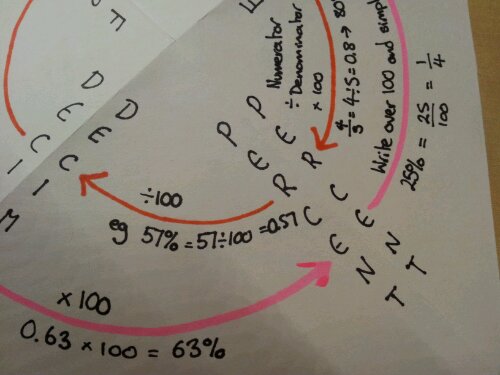
Those of you who follow this blog will know I have a thing for explaining with colours. This isn’t just a gimmick for younger students, it also works for 16-18 year olds.
In the picture below we were looking at proving a statement involving reciprocal trigonometric functions and fractions. A common source of misconception with this kind of question is that students split the question into working with the numerator and denominator separately, then make mistakes when they put them back together. They can’t see the big picture.
 Image credit: Mathssandpit
Image credit: Mathssandpit
When I discussed this on the board I used separate colours for the expressions in the numerator and denominator. The class could follow the logic so easily. It’s probably my most successful introduction to this topic. I saw that some students used highlighter on their notes after I’d gone through it, so they could track the solution.
The second type of question we looked at was solving a trigonometric equation. The straight forward expansion was all in one colour, but the roots of the quadratic were highlighted in different colours. The reasoning behind this was that students often solve half the quadratic and neglect the other impossible solution. Our exam board likes to see students consider the other solution and formally reject it. It makes the solution complete. By using a colour, the impossible solution stands out and reminds students to provide a whole solution.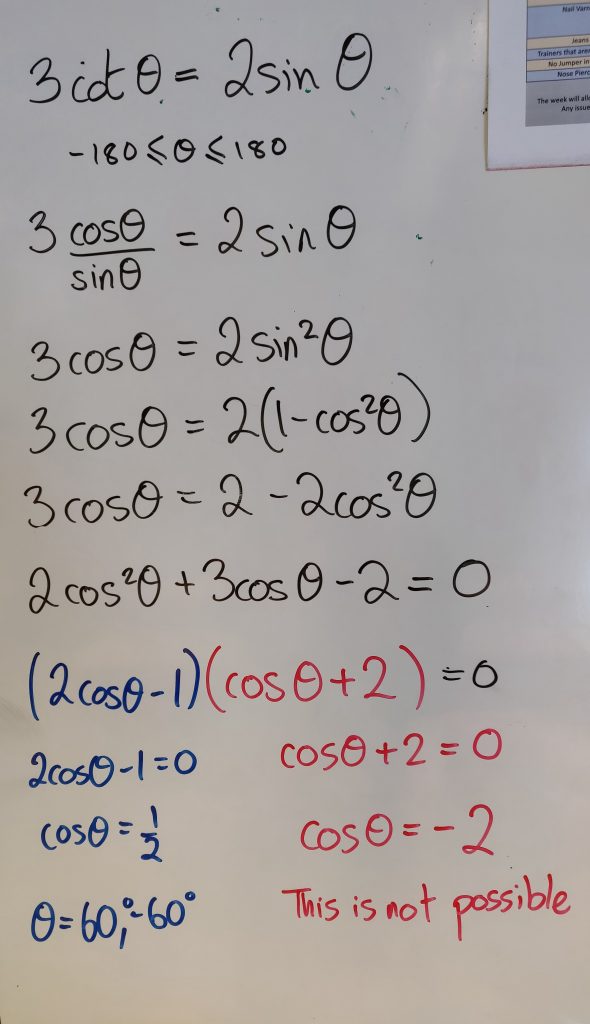
Image credit: Mathssandpit
So when you are planning for misconceptions at A-level, remember that coloured pens aren’t just for younger students.
Update: 22nd October
The brilliant Mr B has shared how he uses colour to identify the forces in perpendicular directions in Mechanics.