It’s our first birthday at the MathsSandpit and this post is party themed. Remember a few years ago, when chocolate fountains were the ‘in thing’ at celebrations and parties. The healthy guests stuck to strawberries drenched in chocolate. The unhealthy went for marshmallows on sticks and … well … all I’ll say is Geraldine Granger (Vicar of Dibley – Chocolate Fountain)

I’m trying to decompartmentalise the maths in my students heads. They struggle to see the links between different topics. So I introduced ‘Marshmalllow Maths’ – they were intrigued/hungry as soon as I mentioned it.

Equipment

• Cocktail sticks
• Pink and white marshmallows

Step 1

Ask your class to connect the marshmallows together

 

Step 2

What mathematical characteristics do the marshmallows have? I’ve summarised my classes’ responses below:

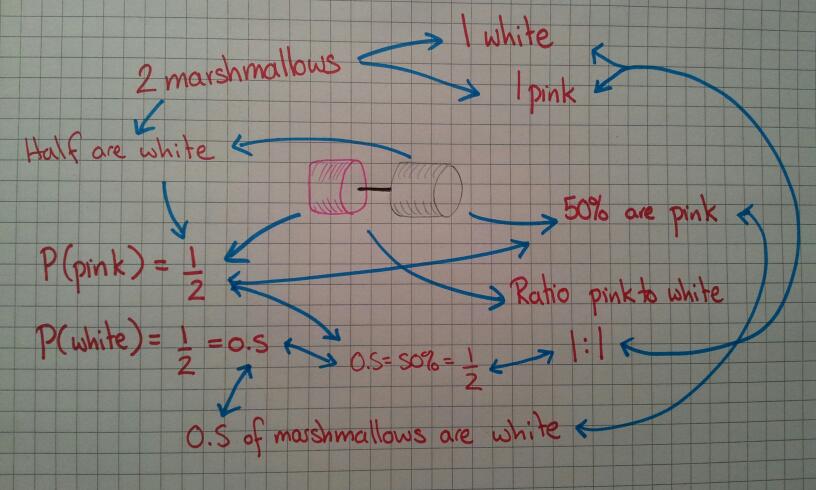
Two marshmallows lead to ratio, percentages, fractions, decimals and probability. The links between these topics start to emerge.

Step 3

Add on another marshmallow

How have the ratios, fractions, decimals, percentages changed?

 

Step 4

Make another 1:2 ratio marshmallow, identical to the previous one. How have the mathematical facts changed? In fact although the numbers have changed, the proportions have stayed the same which is proved when you simplify the numbers. Physically you can prove it by stacking the structures on top of each other – from above it looks like the original structure.

At this point I went cross-curricular and discussed the similarities between the marshmallow structure and water (H20). I was going to label the marshmallows with H and O, but my food-colouring pen wasn’t working. My logic was that water always has hydrogen and oxygen in the same ratio – this means we know we can drink it. If the ratio suddenly changed to H2O2, we would be in trouble! As far as I can remember H2O2 is hydrogen peroxide and is better for bleaching than drinking. This actually got the idea across quite well – no-one tried to fudge their ratios.

 

Step 5

I then allowed the class to make their own simple structures using their own piles of marshmallows. They had to make at least three identical structures, work out the related maths and prove that their numbers could be simplified to the basic form. In doing so they also looked at converting ratios to fractions and also found fractions of amounts.

 

Step 6

Eat marshmallows (whilst doing some related questions).

 

Optional: Step 7

Calculate the percentage increase in body mass on results day! It was marshmallows today, a chocolate prize for cracking a code earlier in the week and they say they learn better when they eat. I think it’s all a ploy to scrounge more food … but if it works … maybe fruit next time!