Tag Archives: Area

365. Area of a sector structured questions

Leave a reply

Image credit byjus.com

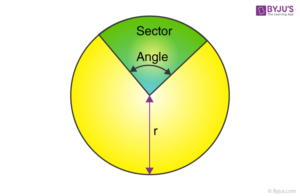
Believe it or not this worksheet has been sat in my Inbox since November 2016. I clicked on it and discovered this structured worksheet on finding the area of a sector, just in time to use it with my Year 9 class.

Area of a sector worksheet (pdf)

Area sector answers (pdf)

It worked exactly as I hoped, if not better. The structure helped students develop their skills. The check column ensured students used the exact value form. Interestingly simplifying the fractions caused the biggest issue – just out of practice. I’d recommend doing some work on equivalent fractions and simplifying as a retrieval activity before doing the sheet.

315. Mancunian Shapes

Leave a reply

I’ve been at a meeting in the Manchester Chamber of Commerce today and I was fascinated by how sympathetically the building has been renovated and preserved. The plasterwork, tiling, glasswork and carving demonstrated exquisite use of shapes, symmetry and tessellation. Here are a few images that you could use as discussion starter:

Just think of all the shape related problems you could set from each image!

310. Menseki Meiro Area Maze

Leave a reply

Menseki Meiro puzzle books crossed my Twitter feed a few months ago and I took the plunge.

Menseki

Image Credit: Amazon.co.uk

The problem is I couldn’t find an English language version. The Japanese originals were expensive so I bought the Spanish version. I don’t speak Spanish so asked my Spanish first language student who said it wasn’t Spanish – she suspected it was in Catalan!

But back to the Menseki puzzles …

They are ingenious puzzles where you simply use your knowledge of the area of a rectangle to solve the problem. Click on the image to see the cover problem. Puzzle 1 was so straightforward a nine year old could do it, puzzle 99 had Y13 Further Mathematicians befuddled. They make perfect starter or plenary activities for any age or ability.

Solutions are provided and if your copy is in a different language, like mine, you might just expand your mathematical vocabulary.

Whilst looking for a suitable image I also came across Alex Bellos discussing them on The Guardian website. Worth a look!

(By the way – the Menseki book also makes a good birthday present for that special geeky someone)

 

250. Crack the Circle

Leave a reply

Here’s a quick resource for consolidating and revising the area and perimeter of circles and semi-circles.

Circles Crack the Safe (pdf)

Pupils complete the worksheet then work out the code. I personally like having a clear glass Kilner-style jar with a combination padlock at the front of the class … with a little treat for the class to aim for securely locked inside!

248. Fair decorations

Leave a reply

Here is a quick cake conundrum for you.

image

Two girls are decorating the christmas cake. It is a square fruit cake. They share the icing such that one girl ices the top and one face. The other girl ices the remaining three faces. What possible dimensions of the cake will make the icing areas equal?

245. Fair share

Leave a reply

I spotted this ‘Expert Tip’ whilst flicking through a supermarket magazine:

image

Image credit: tesco.com/foodandliving

Question
If this cake has a diameter of 18cm (7in), is this a fair way to split it between guests? Can you prove your result in general terms?

Of course, this assumes that the icing on the side doesn’t count in the diameter or guest preference.

216. Back to the Takeaway

Leave a reply

If you like Takeaway homeworks or need a resource for the area and perimeter of circles, including some arc/sector challenges, then my third takeaway homework is for you!

Takeaway Homework 3: Area & circumference of circles