With the exams looming large, I thought I’d share how my class have been revising. To give you some context roughly a third of the class are doing Foundation GCSE, aiming for at least a Grade 4. The rest are doing Higher and aiming for a Grade 5 or better. We have three, one hour, lessons a week. I’m rotating between doing an exam paper, a whole class revision activity (eg a revision clock) and tiered revision.
I know if I tell the students to revise independently the results are going to be mixed. Some will be brilliant, some will be more laid back. To resolve this I pick a topic (or two) from each tier that I know they need to improve on from or that they have requested. It’s helpful if there is a theme to the work. I’ve recently done things like y=mx+c (F) with plotting inequalities (H).
Now the genius part: PixiMaths revision jotters
How to run the session
Photocopy a big stack of revision jotters. If you are doing black and white copying, use the b&w version. We requested the b&w version and, because PixiMaths is awesome, it is now on the website.
Clearly put on the board which topic each tier is revising
Eg Foundation: exact trig values, Higher: trig graphs
Give students 5-10 minutes to fill their revision jotters with everything they know. Have textbooks or maths dictionaries available to fill in the gaps. You may find that Higher students want to do the Foundation topic too – no problem, just make sure they have two jotters. Due to the complexity of the Higher topic, they will need more time to make initial notes.
My students are allowed headphones in revision sessions. At this point it’s headphones in for Higher and out for Foundation.
Do a skills recap on the board (exact trig values), with maybe an exam question too. Students can ask questions on the topic and add to their jotter. Then have a worksheet for students to do eg Corbett Maths or KeshMaths GCSE exam questions booklets. They can refer to their revision jotter or scan the Corbett Maths QR code for extra help.
Swap over. Headphones in for Foundation and out for Higher.
Repeat the process for Higher, with drawing trigonometric graphs. Issue an appropriate worksheet.
Once you’re done, make a judgement call. Are there students who could push it further? Maybe transform a trig graph or problem solve? Go for it. Foundation are busy, Higher are busy, spend some time stretching your most able. Every mark counts.
A huge thank you to PixiMaths for the revision jotters (and everything else).
Examples of students’ work
Shared with permission of students. You can see that they have personalised them to meet their needs and some are a work in progress. Also, the b&w jotter photocopies so nicely.
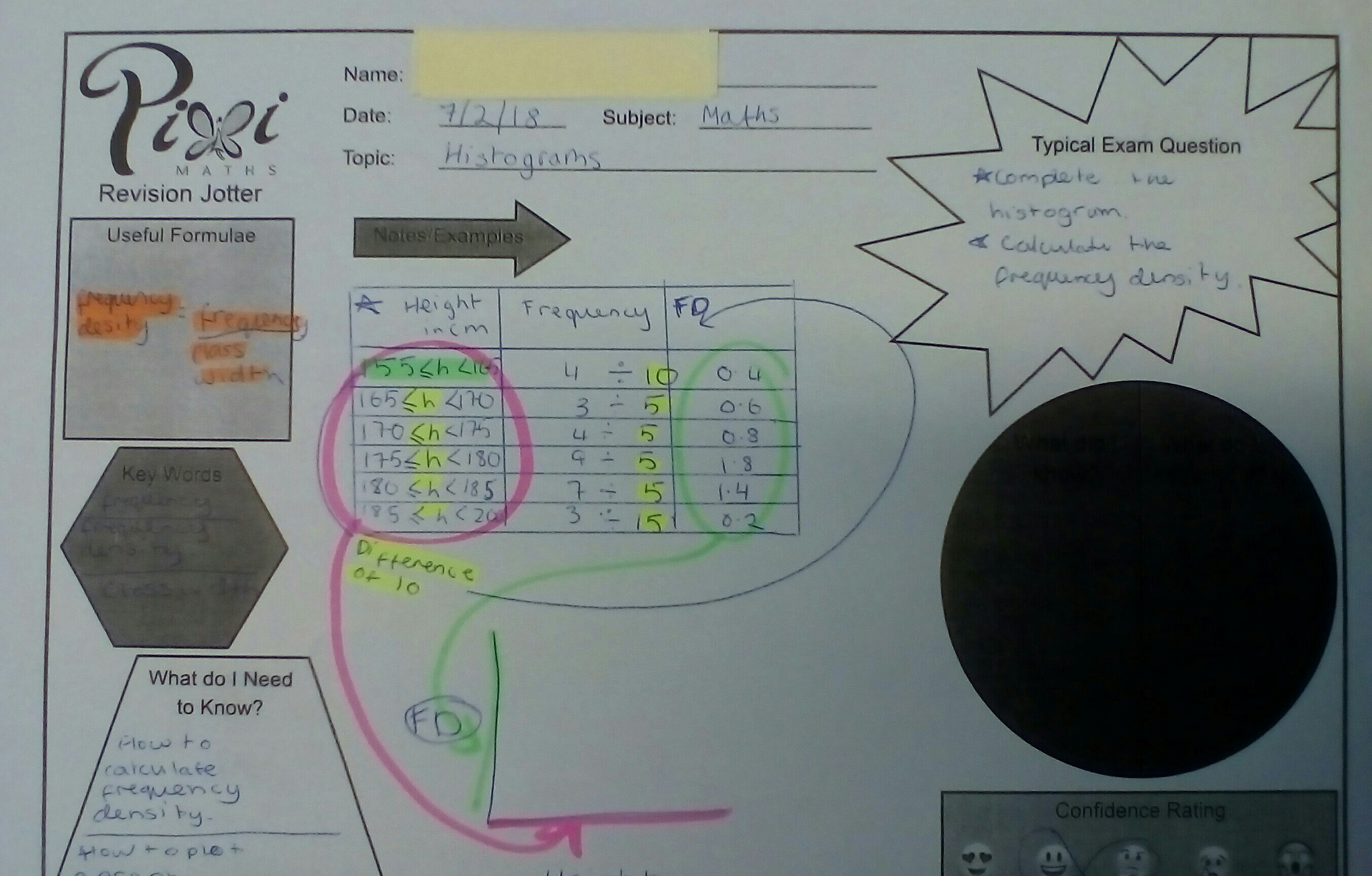
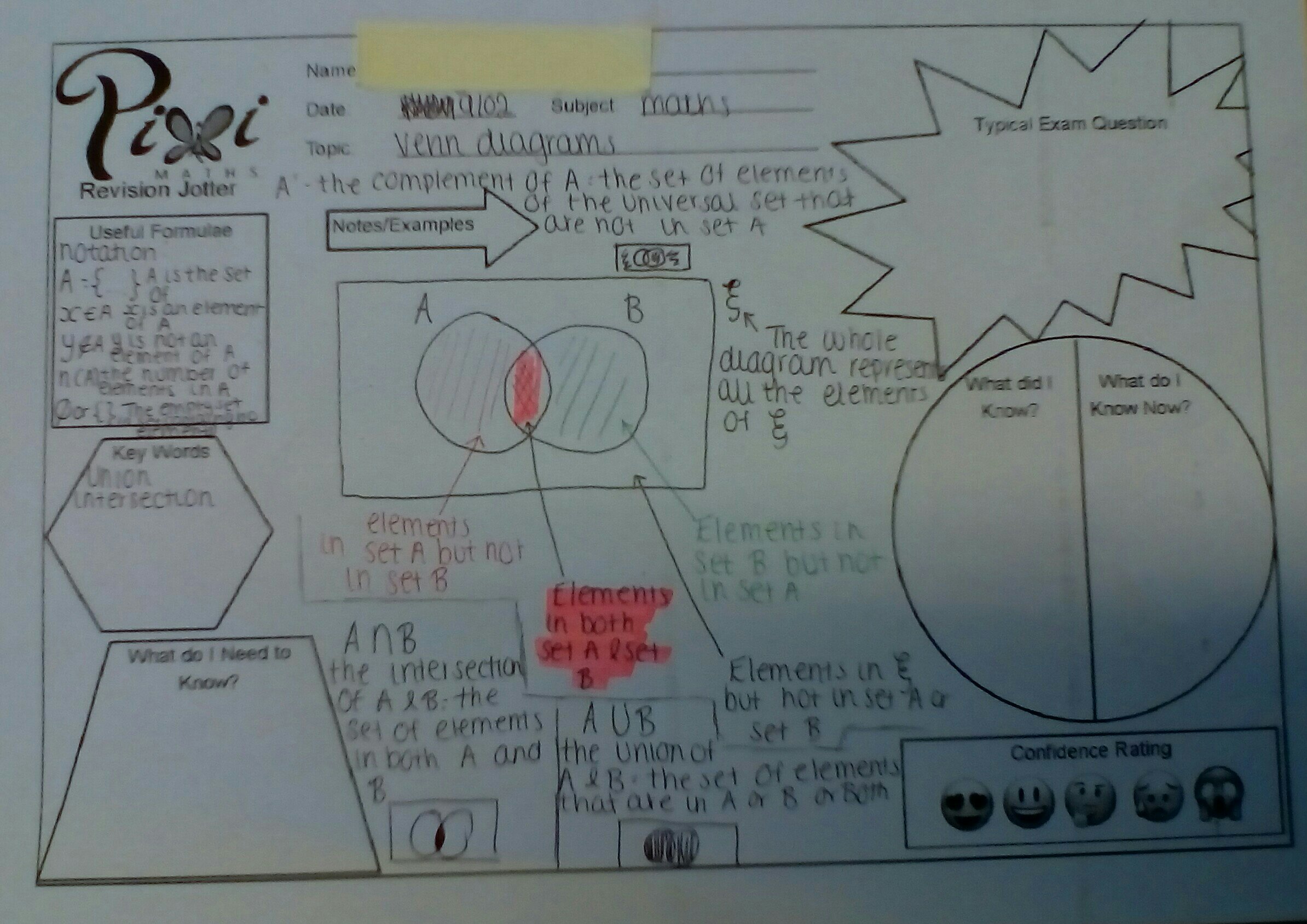
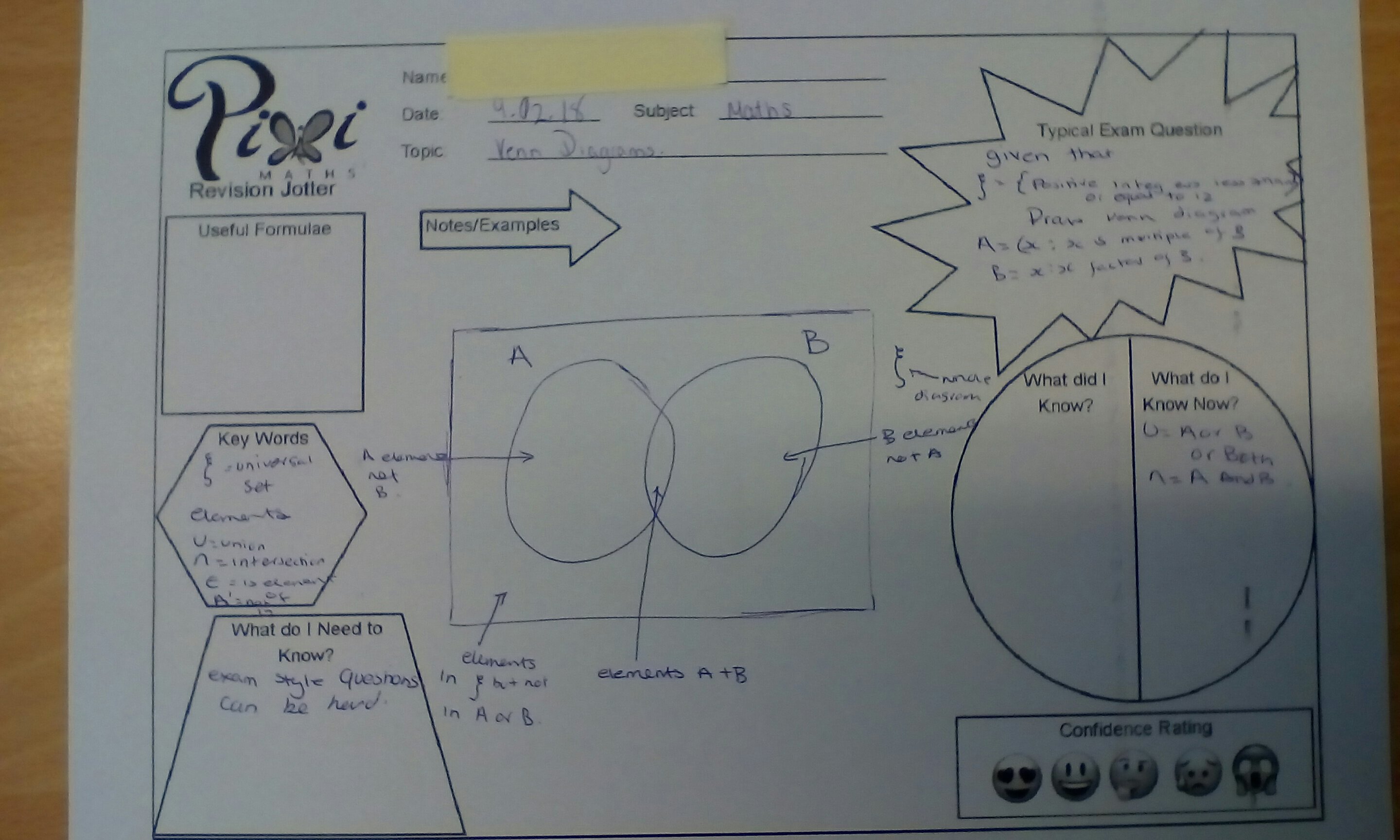

Like this:
Like Loading...