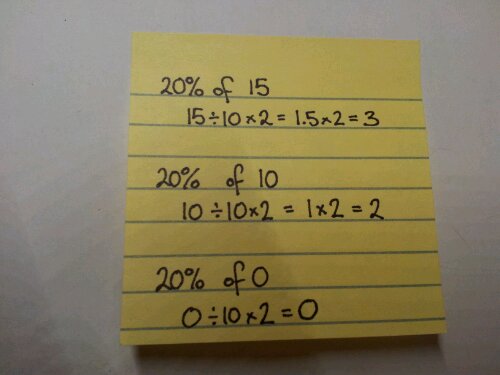It’s perfectly obvious that fluency in the use of multiplication tables directly impacts students ability to divide. This grows into confidence with algebra and reverse operations. Students are able to see the links between the concepts. Our understanding of the importance of such skills is part of the success of programmes such as TTRockstars and Numeracy Ninjas.
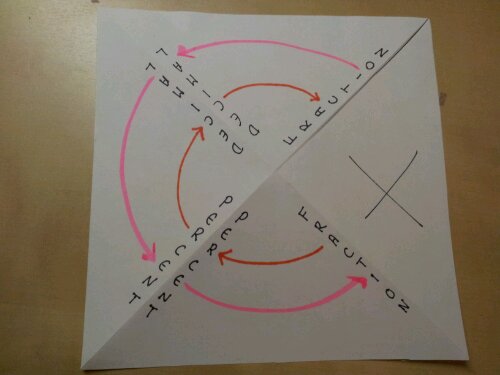
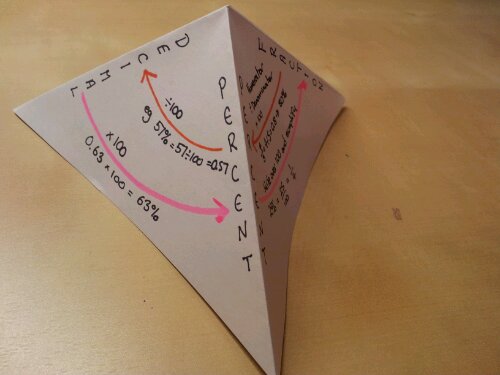
Why is it then that so many textbooks, websites and resource banks keep the manipulation of percentages as separate skills sets? Percentage increase / Percentage change / Reverse percentages. We know that when concepts overlap, fluency increases when these links are pursued. So that’s what I set out to do.
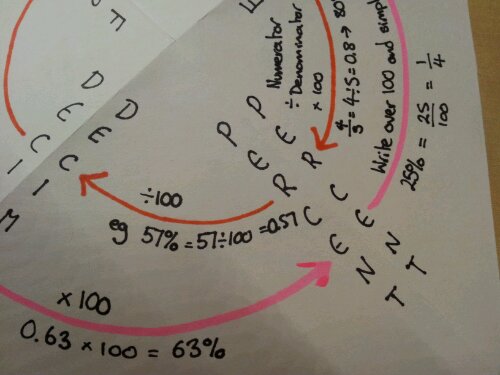
I have a bright Year 8 class and started working on percentages with them. It didn’t take much to have them confident using equivalent decimal multipliers to find percentages of amounts. Using a multiplier for increase/decrease was a walk in the park. Then finding percentage change came up. Over the years I’ve seen a lot of students get very confused with half remembered methods:
“Which do I take away?”
“What number do I divide by?”
“Is this calculation the right way around?”
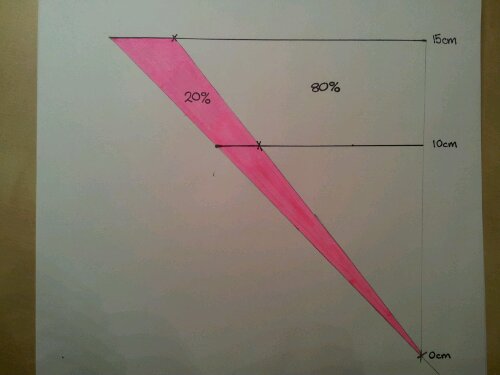
I tend to teach new value divided by old value and interpret the answer. It got me thinking – why am I teaching them this? They can increase by a percentage using a multiplier, why can’t they rearrange their working to find the actual percentage? Same goes for reversing a percentage.
After a good discussion, I used this worksheet to recap and develop their skills:
Percentages Linking concepts questions
Percentages Linking concepts answers
Warning: “Original Amount” section, question (d) is a tricky one.
As with all new approaches, it’s always good to see if it worked. I set the following task from Don Steward’s website:
I have GCSE students who wouldn’t know where to start on those questions, yet my Year 8 with their ‘have a go’ attitude were absolutely awesome. I’m definitely using this method again!