It’s been a while, but I’m back. Crazy times and all that!
Today I’m sharing a presentation about my thoughts on the Edexcel A-Level Maths papers, from the perspective of reviewing students papers. As a KS5 Co-ordinator I am asked by students to look at borderline papers before they send them off for a paper review.

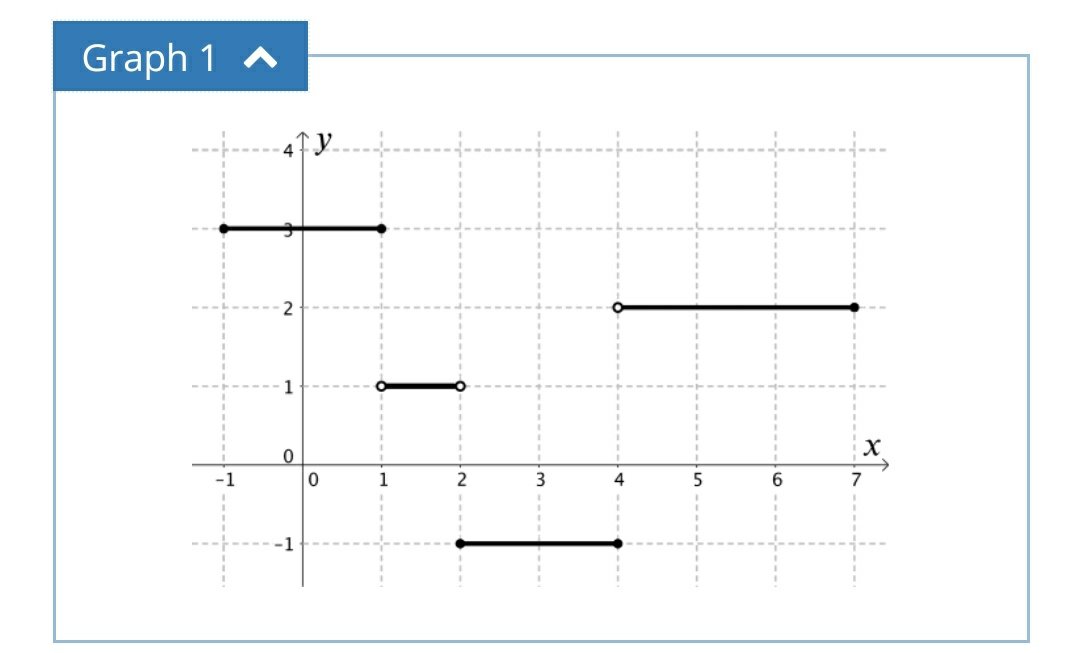
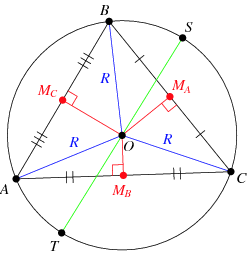
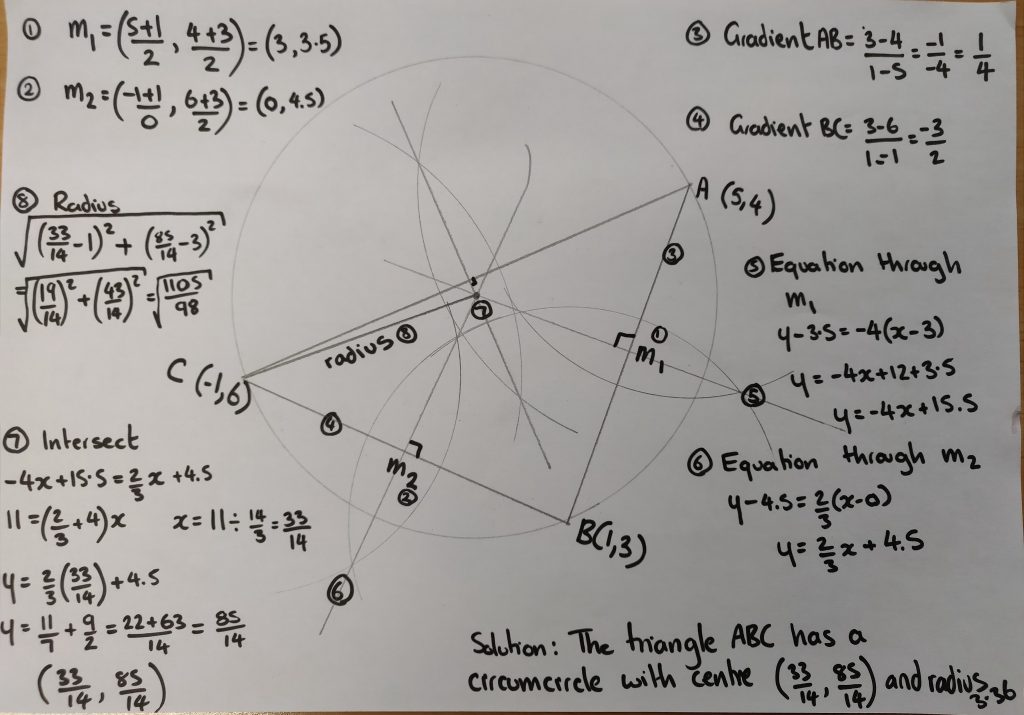
The mark schemes were very clear on where marks should (or should not) be awarded. This presentation (or set of posters) highlights the most common student errors I spotted during my reviews. I would also say that these are most frustrating issues as they are so easy to fix. Unfortunately it highlights the lack of formal external exam experience this cohort had, through no fault of their own.
These resources are geared towards the Edexcel papers, but I’m sure the skills are equally appropriate for other boards. Also a hat-tip to Jack Brown & TLMaths as I have linked one of the misconception slides to his video on hidden quadratic equations (thank you!).
Exam misconceptions 2022 (PPT editable)
Exam misconceptions 2022 (PDF)
Personally, I’m going to print these out and put them in my A-level display corner. I might use the actual presentation after the Y13 mocks to see if they’ve fallen for the same issues. I hope not!