If you haven’t discovered the BBC ‘Infinite Monkey Cage’ podcasts yet you are missing out on a scientific treat – oh, and it’s presented by Brian Cox & Robin Ince.
Monthly Archives: February 2013
24. Foundation GCSE student review
This idea came about after a Departmental INSET on teaching the C3 unit run by my HoD.
Students never believe you when you tell them they must understand this topic as it’s an essential skill for their exam. So get them to tell you what is important…
Before you start
You will need a different GCSE paper for each student (I used Foundation non-calc). It is possible to use one between two.
You will also need pens, scissors, glue & display paper in four colours.
Cut and label
Each student cuts out the individual questions and labels them with the month & year eg Jan 12.
Sort 1
Each student sorts their questions into Number, Algebra, Data, Shape.
Sort 2
Assign each area of study to one of the sheets of display paper. The students pile their Number questions onto the Number sheet etc.
Categorise
Split the class into four groups and give each group one area of study to look at. They must sort the questions into common themes eg BIDMAS, sequences, pictograms.
Review
Ask each group what they notice eg in most exams there is a question related to drawing/reading a bar-chart.
Display
Each group sticks the questions down and labels the common themes.
The class spotted all of the common themes and key skills, without me turning into a nag. As you can see from my wall display, we needed an extra sheet for number questions. The foundation GCSE paper has 40% number questions, which equates to 2/5 of the exam – our work was spot on. During the revision sessions I have referred to this wall display frequently. It has also been a talking point for other classes.
Update
Mark Greenaway (@suffolkmaths) has made an instructional to go with this idea. Go to his website www.suffolkmaths.co.uk and select ‘Exam Advice – Supporting powerpoint’ to see it.
23. Coffee overload
I was sat in a coffee shop when I overheard the barista say to a customer ‘Take your time, there are about 20,000 different drinks available’.
Sounded like a mathematical challenge to me.
If the menu below was real, how many different drinks could made?
How many would be drinkable?
Size: S, M, L
Drink: Filter, Americano, Cappucinno, Machiatto, Latte, Espresso, Hot chocolate.
Coffee type: Decaf or caffeinated
Flavour: Vanilla, Mint, Hazelnut, Ginger, Caramel, None
Milk: None, whole, skimmed, soya
Hint: Be methodical, work out the hot chocolate options first.
Solution
Hot choc
Size *Flavour*Milk = 3*6*4 = 72
Coffee
Size*Drink*Type*Flavour*Milk =
3*6*2*6*4 = 864
Total number of drinks
864 + 72 = 936
This doesn’t consider extra shots of coffee or syrup. Imagine how many variations there are in a big coffee shop!
Me … I’ll have a black filter, no milk, no sugar.
22. Free Geogebra download
21. Multiplying 6×6 to 10×10 on your fingers
This is a great video from Youtube:
20. Polygon Challenge
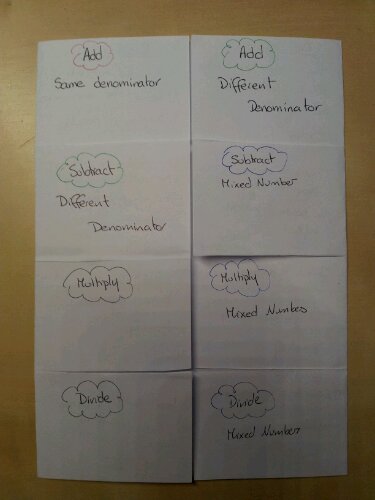
19. Fraction Skills Foldable
This resource was designed to recap basic fraction skills as part of KS4 revision. The foldable covers:
1. Addition with common denominator
2. Addition with different denominators (butterfly method)
3. Subtraction with different denominators (butterfly method)
4. Subtraction with mixed numbers
5. Multiplication
6. Multiplication with mixed numbers
7. Division (reciprocal method)
8. Division of a whole number by a fraction
It also deals with equivalent fractions, simplifying and converting between mixed & improper fractions.
Each section has a title, method and example.
This is a draft ‘teacher’ version. My students made theirs look really good with different colours, highlighter and their own examples.
Note: this isn’t for teaching a full understanding of fraction manipulation, just summarising facts.