Speed Cameras are so last century: discerning law enforcement agencies favour the Average Speed Camera!

These motorway delights timestamp when you go through certain checkpoints and calculate your speed between them. No complicated laser guns required, just number plate recognition and a little distance/time calculation. This already sounds like a KS3/4 class activity or a Mechanics A-Level starter.
Equipment
Squared paper
Pencil
Ruler
Coloured pens
Calculator (optional)
Question
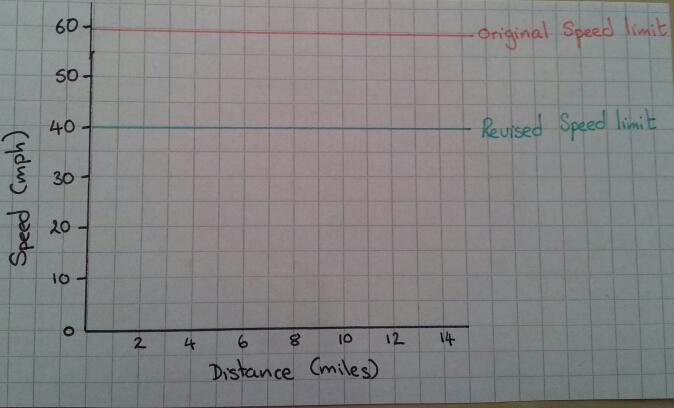
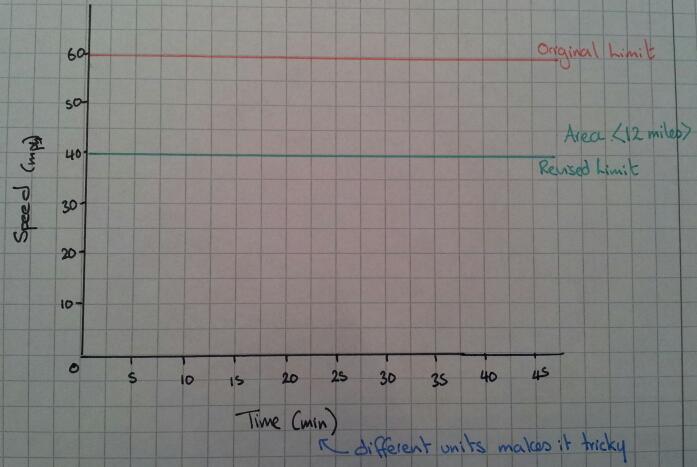
Can you find three different (safe) strategies for staying on the right side of the law through extended roadworks? You must average 40mph over 12 miles (original speed limit 60mph).
Visual Prompt
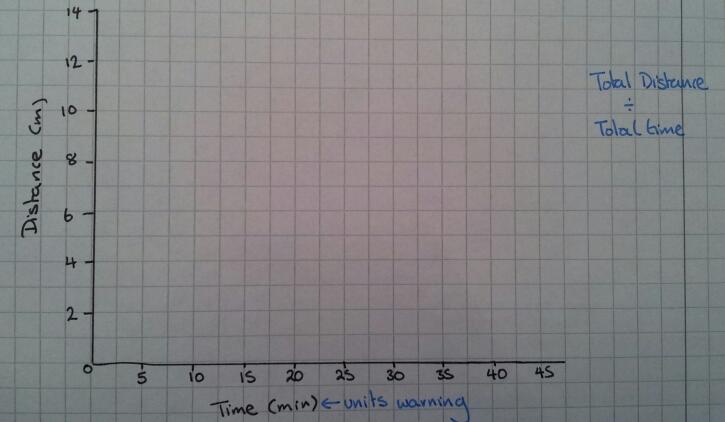
To start off with just draw out blank axes and discuss how you could visually represent this problem.
Idea 1
A distance-time graph
Idea 2
A speed-distance graph
Idea 3
A speed-time graph
The straightforward option
How long should it take you to get through the roadworks if you stick to exactly 40mph? What does this look like on a graph? Which type of graph shows this information best?
Top Gear Alert
The boy racer wants to go fast, but avoid a ticket – what could he do?
Hint
What does ‘Average Speed’ actually mean?
Can you instantly jump between speeds?
Is acceleration going to effect your calculations?
What assumptions should you make about acceleration?
Do you need to work out the area under the graph or the gradient at all? How will you do this?
Can you describe what is going on?
Is it safe/legal?
Outcome
Your students should be able to produce many different graphs of how to stay on the right side of an average speed zone. They should be able discuss their findings with each other. However the morality or safety of their driving ideas may be a topic of discussion for a later PSE lesson …
Like this:
Like Loading...