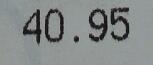Simple little starter for you today. Minimum preparation, personalised challenge.
Equipment
- Paper or whiteboards
Instructions
- Hand out mini whiteboards or use paper.
- Write the alphabet on the board.
- Assign each letter a value. You can go for the standard 1 to 26 or choose a mixture of big/small numbers – maybe a negative number or two.
- Get each student to write down their name and associated numbers.
- Write a target number eg 100 on your board.
- Each student must use the numbers of their name to make the target. If they can’t, they must get as close as they can.
- If they make that target either find another way or change the target number.
- Alternatively once they’ve finished they could use their classmate’s name – did they use the same method?
Variations
- You can make this as easy or difficult as you want by changing the target or the alphabet numbers.
- Throw in some fractions or decimals – go all the way and thrown in algebraic indices or standard form. You are the best person to judge your students’ level of challenge..
- You could allow surnames, you could insist all numbers are used.
- Put three alphabet variations on the board for mixed ability teaching.
- If you are teaching a class not in the English language (eg Welsh, Greek, Russian), where the alphabet is different, this still works just assign each letter/character a number in the same way.
- The possibilities are huge – have fun!
Note: this isn’t numerology, it’s proper Maths!