My (not so little) monkeys in KS3 have been discovering and using Pythagoras’ Theorem. They usually deal with open questions quite well, however this one took a fair bit of discussion. This challenge requires no worksheets or fancy resources, just write it on the board. The context is modified, but the essential question remains the same.
Challenge
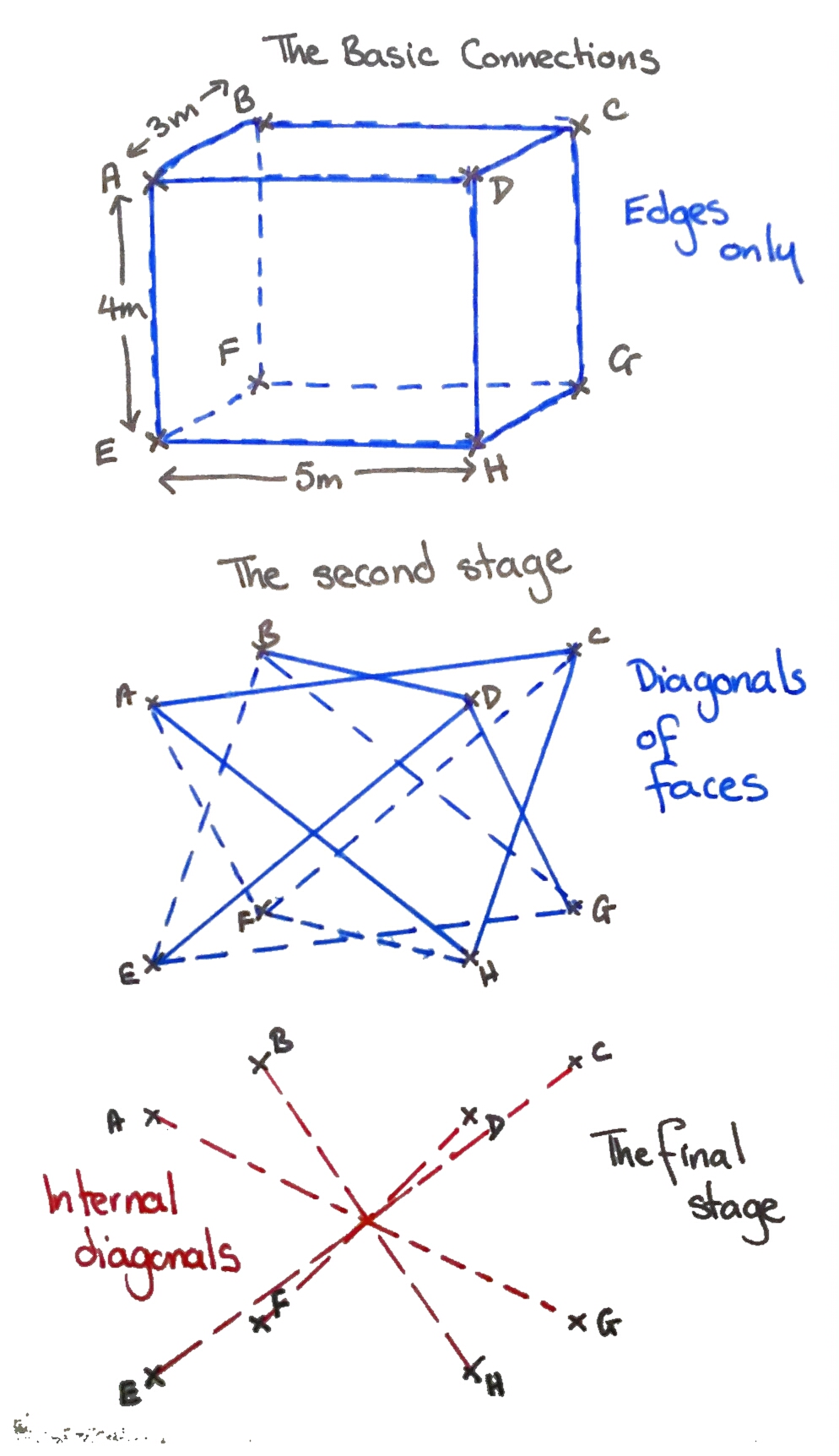
Zookeepers have attached eight bolts in a cuboid formation (sides 3m, 4m and 5m) to the trees in a chimpanzee enclosure. The keepers attach taut ropes between the bolts for the chimps to climb on. Each length of rope is individually cut. No length is lost in knots.
- What is the maximum length of any one piece of rope?
- What is the total amount used, if every corner is joined without duplication?
Solution
The first step to solving it is a good diagram of the problem. Students then need to break it down into triangles. The solution has several levels of difficulty:
- Total of the edges of the cuboid
- Total of the diagonals on the faces
- Total of the diagonals across the inside of the cuboid
This diagram demonstrates the levels of the problem – have fun!