Tag Archives: vector

284. All tied up – an adventure in skewness

Leave a reply

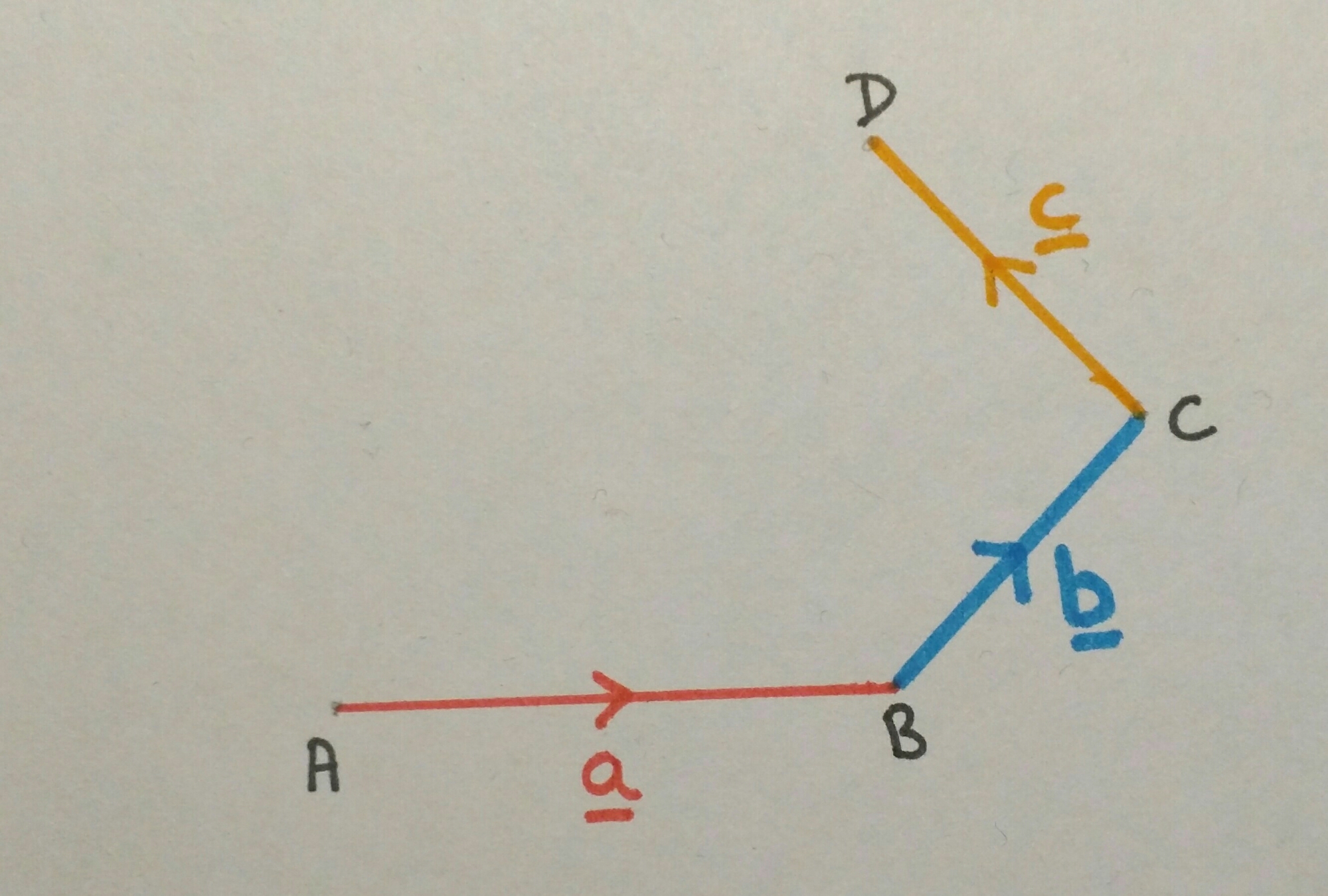
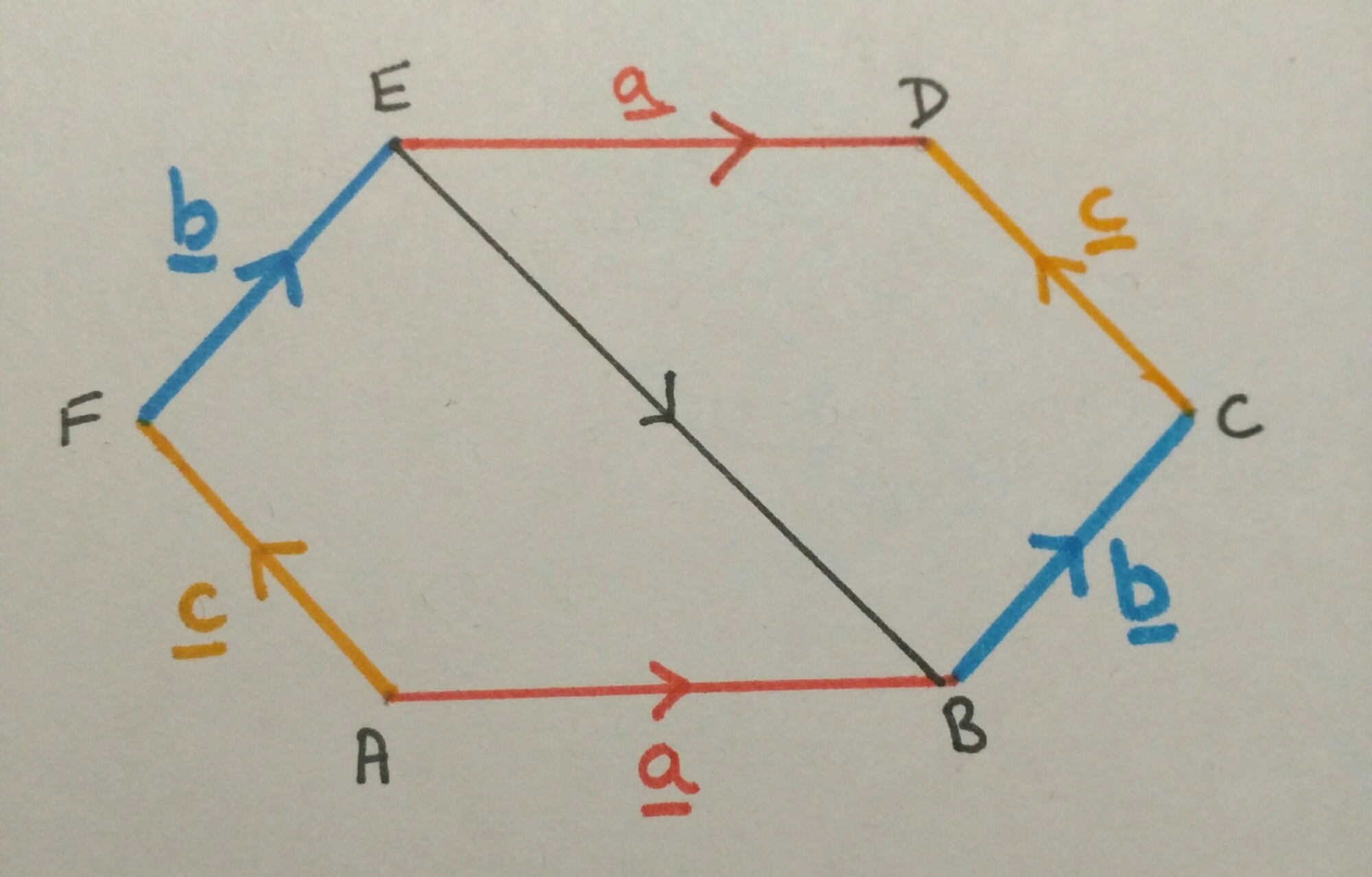
When you move from 2D vector equations to 3D vector equations the biggest challenge is skewness. On plain old 2D graphs if two lines aren’t parallel, they intersect and vice versa. Not so easy in three dimensions … how to explain skewness? Got some string and duct tape? Then let me explain …

Equipment
String
Scissors
Duct tape
A low ceiling
A chair/stepladder/tall student

Step 1
Tape a piece of string from the ceiling to the floor at an angle. Attach a second piece to the ceiling and ask students to position it so it is parallel with the first string. This isn’t as easy as it seems once they realise it must look correct from every angle. Secure the string to the floor with duct tape.

Step 2
Attach a third piece of string to the ceiling. Instruct students to position it so it intersects one of the strings. Secure the end.

Step 3
Attach a fourth piece of string to the wall. Ask them to position it so that it is not parallel to or intersecting any existing string.

(My ingenious bunch took the string out of the door and fastened it to the bannister, just in time for management to thankfully not be garroted)

Step 4
Give the students a fifth string and instruct students to make it parallel to an earlier string and intersect the fourth string. They choose both end points.

If all goes well, you’ll get something like this:

image

You can then explain the differences between parallel, intersecting and skew lines without resorting to iffy diagrams on a whiteboard or complicated geometry software. Students can walk through them and really get a feel for the geometry of the situation.

(When it comes to taking it down, I hope your students are slightly more sane than mine – one of them shouted ‘Argh, it’s a spider web’ and ran through it. Actually quite an efficient way to tidy up!)

Resources
You can download five large print 3D vectors here:
3d vector cards (pdf)
3d vector cards (docx)
The challenge is to find the parallel lines (3 lines), the skew lines and the intersecting lines (2 pairs).

There are more ideas on 3D vector equations here:
211. Hidden Rectangle Problem

266. Jump into a vector

2 Replies

This activity is the Joey of Maths teaching!

Joey? Why yes! Joey Tribbianni from ‘Friends’ (random 90s TV reference). When the friends came to London, from New York, Joey demonstrated his unique technique for navigation:

He jumps into the map! And that is what my students did for vectors.

In the first lesson we started looking at the basics of vectors. I found this PowerPoint from TES resources to be really good for starting discussions:
Introduction to Vectors by rhemsley

In the second lesson, we started to solve problems and moved outside.

Objective

  • To develop problem solving skills with vectors.
  • To understand how vectors relate to more complex diagrams

Resources

  • Chalk (coloured is good)
  • Vector questions from a textbook, worksheet or exam database
  • Mini whiteboards – optional for working out/calculations on the move

Activity

I drew one side of a regular (ish) hexagon on the wall (I really would like an outside chalk board). We labelled the ends A & B and the vector joining them was a. I decided to use a different colour chalk for each vector to make them stand out.This was followed by vector b (joining B & C) and vector c (joining C & D). To be honest, I had to get a student to draw in D and the line – I’d accidentally* drawn the diagram higher than my arm reach.
image

(*I’m over 5ft 6in, but my lively lads are nearly 6ft – gallantry meant they felt they had to help and hence engaged with the task very quickly!)

Back to the problem:
This hexagon wasn’t going to draw itself, but which of the existing vectors to use to create point E? I explained that vectors a, b & c are our building blocks, which helped us move on.

The students were quick to identify vector a. They were very picky about the direction too. My gallant helpers added it to the diagram. We used the same logic to finish off the hexagon.

image

The students then went away with their worksheets and drew out their own versions of this diagram. As I walked around there were some heated debates as to which vector went where and in which direction. They addressed many misconceptions before they even looked at the question – it comes back to the old rule of ‘ Write down what you know’. They’d already answered questions on the diagram that they hadn’t yet been asked.

The questions were based on this diagram:

imageThey started easy and quickly moved on to trickier concepts:

  •  Why can’t you just invent a letter for BE?
  • Does it matter which route you take around the diagram?
  • Can vectors be simplified like algebra?

All of these questions can be solved by ‘doing a Joey’.

When I teach vectors I always use the analogy that vectors are like a one-way system of roads. For example, the vector from E to B is drawn in, but has no specific vector – this is like a closed road, you must detour down the other roads to get there.
As you walk down the other roads (vectors), are you going the correct way?

  • If the answer is ‘yes’, just make a note of the vector and carry on.
  • If the answer if ‘no’, then a minus sign gives you the permission to go the wrong way – write the the vector with a negative. (This then leads to the follow up discussion of why this works through use of column vector examples)

There is more than one route. What do you chose?

  • Clockwise or anticlockwise?
  • EDBC or EFAB?
  • Walk them both and see what happens – you can see that the vectors are the same, just arranged differently.

Finally, when you start to compare different routes, you can see that vectors cancel out, just like algebra. In fact, it quickly becomes clear that basic rules for simplification still apply.

Student Reaction

The sight of pupils walking around diagrams looked like something from a Monty Python funny walk sketch. As we walked back to class, after half an hour in the sun, I overheard two different groups of students. One group said: ‘That was a really good lesson’ and ‘Yeah, I enjoyed that!’ – that may have been the sunshine though. Another group however said: ‘I get it now. I didn’t get it last lesson the board, but now I get it!’ – and that wasn’t just about the sunshine!