Category Archives: Problem Solving

139. Maths Roast

Leave a reply

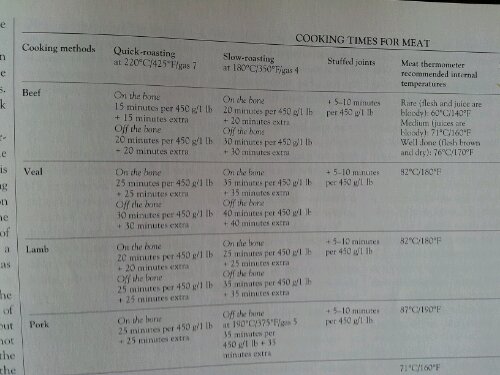
We’ve all seen the question about using a worded problem to work out the cooking time of a chicken. So dull and in many respects irrelevent – cook books & websites don’t write a big description. This is more like real-life:

Extract from the ‘Reader’s Digest Cookery Year’

image

Butcher’s label – no cooking instructions

image

Equipment
Pictures of labels from fresh meat* (actual labels are a hygiene hazard) – you might want multiple copies
Some cookbooks or tables of temperatures for cooking
Cards saying ‘Delicious’ or ‘Food poisoning!’
Calculators
*Be aware of pupils’ beliefs regarding meat – you don’t want to cause offence

Activity
1. Give out the cooking instructions & labels from the meat, ensuring the actual type of meat is on them.

2. Get pupils to decide how they want to cook their meat. You may also want to specify the cooking method to ensure variety in the,solutions.

3. Pupils calculate the appropriate times.

4. Each person (or group) presents their answer to a group (or the class). The other pupils hold up ‘Delicious’ if they agree or ‘Food poisoning!’ if they disagree. This can lead to a discussion as to why.

5. This can then be extended to look at writing formulae for cooking times.

Vegetarian Option
This task is easily adapted for any vegetarian recipe where weight is important eg Roast squash.

Don’t forget all the work on time and unit conversion that can be included!

138. Kandinsky Combinations!

Leave a reply

This week I gave a talk to a group of PGCE/Schools Direct associates about innovation and ‘keeping it fresh’. One of my points was you should ‘Keep the good ideas and bin the rubbish/pointless ones’. This is one of my ideas I kept – first used in the late 1990s!

Background
Wassily Kandinsky was an artist, born in Russia in 1866. He died in France in 1944. He is credited with being the first artist to explore purely abstract work. Researching him is a nice homework task which can add to the final work.

Farbstudie quadrate mit konzentrischen ringen

image

This work has been reproduced thousands of times -you can see it everywhere from student bedrooms to upmarket coffee shops. The original was completed in 1913. It roughly translates as colour study squares with concentric circles.

Investigation

You will need:
Squared paper (or plain)
Coloured pencils or pens

1. Show the class the painting and discuss how the colours are arranged.

2. How many ways can you colour in one square with one colour? 1

3. How many ways can you colour in two concentric squares with two colours? 2

4. Repeat for three colours and ask for predictions. The usual prediction is 3, the answer is 6.

5. Repeat the process and ask them if they can see a pattern forming. Encourage them to be methodical.

The colour patterns form a set of factorial numbers. Finding out about factorials could be a good extension task.

After the work is completed you’ve potentially got a great wall display, a cross-curricular link to art and an understanding of combinations/factorials.

Variation
This also looks rather cool done with concentric equilateral triangles or hexagons on isometric paper.

134. Revising around in Circles

Leave a reply

Ah … beloved GCSE students. Why does revising feel like I’m just reteaching a topic for the Nth time?

image

I’ve been trying some new ideas out on my GCSE group. One of the more popular ones ideas, for an unpopular topic, were these Circle Theorems fact cards. Students were given four cards with a diagram and an open question, for example: What is special about angles ABD and ACD? In the gap, they had to answer the question. They soon realised that the answers they had written were the theorems that they’d learnt. Their solutions had popped into their heads, without being bogged down by number stress. They could then try number questions, referring back to these fact cards if they got stuck.

133. Smart Research

Leave a reply

Teachers often get students to do research homework for one of two reasons: to increase independent learning and develop an inquiry mindset or as an easy homework to set/mark.

Pupils often see research homework in one of two ways: as an opportunity for independent study and to find out cool facts that no-one else will find or as ‘None set’ – the teacher won’t check it and if they do there is the excuse that the computer wasn’t working, the printer had run out of ink, the internet went down or it wasn’t their classes day to use the school library.

How can you change this mindset?

Over the years I’ve set this type of task with varying degrees of success. Conscientious pupils write/type a short essay, with diagrams if appropriate – you could put it straight on the wall to be admired. Others print out webpages or copy a couple of lines from the internet/textbook/friend. Then there is the woeful list of excuses brigade …

This time I changed one thing in the task and I was frankly amazed: 100% successful completion. The change was so simple – how it could be done.

image

I asked them to research letter frequency analysis. Some wrote a page in their book, some took a photo of a page from a book, some did a printscreen and others bookmarked a website. Three of these four formats involve the use of smartphones. Unless your school has draconian rules on mobile phone use in the classroom, this is a good way to engage pupils. It promotes responsible use of technology and prompted discussions on how they’d searched to get their result.

All I had to do was walk around the room and let them show me their homework while they did the follow up task. Cynics might say that they could quickly do their homework before I got to them – this is a valid comment, except the ‘Usual Suspects’ came into the room waving their phones, desperate to show me their work!

BTW I was rather amused when one of the pupils showed me a screengrab of this blog – he didn’t have a clue that I’d written it.

132. Good question, Bad question 1

Leave a reply

I like a topic that you can have fun with and also relates to the big bad world outside the classroom. We are constantly asked our opinions on websites, customer feedback surveys … even personality ‘tests’ in magazines. Every day there seems to be a new set of survey results hitting the news. How can you link a lesson with life?

Instead of telling pupils about biased questionning and surveys, why not give them a week or so to make a note of how often they are asked questions? They can evidence it by taking photographs, screengrabs, cutting surveys out or writing them down.

Task
Mix up the pupils into groups and get them to focus on what the question is asking and how they are expected to answer.

Note
Be prepared for some off topic discussion if they have surveys like ‘Which member of boyband X are you most likely to marry?’ or ‘Have you got what it takes to be the next (insert sportsperson or team manager here)?’

Development
Discuss which questions are fair (unbiased) and which are leading you to a certain opinion. If there are multiple choice answers, do they cover all possible ideas? Think about who would have access to this survey (sampling/sample size).

Challenge
Imagine you work for a website, magazine or shop.
1. Design a fair survey researching opinions on a relevant topic.
2. Design a very biased survey on the same topic.
3. Carry out the surveys on the same people.
4. Compare results.
5. What impact did the bias/unbiased style have?

127. How to save money

Leave a reply

A nice easy question to start the term with:

image

You go to the supermarket to buy your favourite shower gel (or other product). It usually costs £2.99. You have three £1 coins ready, when you notice the price has temporarily been reduced to £1.

What is the most money you can save?

Hint: Think of future gain

Solution:
It’s not the obvious £1.99 saved – that is instant gratification.

It is actually better to buy 3 bottles:

Saving = Actual price x 3 – Reduced price x 3

Saving = £2.99 x 3 – £1 x 3 = £8.97 – £3 = £5.97

If you spent the whole £3 (which is one bottle plus one pence), you get a long term saving which is worth far more, for just 1p more.

Teaching the concept of delayed benefit is rather useful, especially if you are trying to encourage open investigations or looking at time spent on personal revision.

126. Kusudama to meet you

Leave a reply

Wow … September again and many people will be meeting new faces for the first time. Learning names, setting out classroom rules, figuring out who’s got all the textbooks you need …

image Made using origami paper.

Back in July I made Kusudama flower balls with a couple of classes. It occurred to me then what a great ice-breaker they could be. They’d also be a nice maths club project.

Definition of Kusudama from Wikipedia

The Japanese kusudama (薬玉; lit. medicine ball) is a paper model that is usually (although not always) created by sewing multiple identical pyramidal units (usually stylized flowers folded from square paper) together through their points to form a spherical shape. Alternately the individual components may be glued together. Occasionally, a tassel is attached to the bottom for decoration.
Resources

You will need:

  • 5 squares of paper for a flower
  • 12 flowers for a ball
  • 60 squares of paper in total (sugar paper is cheap, but doesn’t tape together well)
  • String if you wish to hang it up
  • Card if you wish to mount a half ball on the wall
  • Sticky stuff: glue sticks or glue dots or pva glue or tape or a hot glue gun – whatever works for you!
  • Beads or ribbon for decoration (optional)

Activity

It has an instructional video and very clear step by step photographs. It’s so easy a six year old can (and did) do it!
image
  1. The instructions assume 30 pupils in a class. Let each pupil make a petal following the step by step instructions and then independently make another (2 petals each).
  2. Pupils pair up and stick two petals together (1 petal each and 1 pair stuck together).
  3. Pairs team up with another pair and stick their pairs together (1 petal each and 4 petals stuck together).
  4. One person in the four uses their extra petal to complete the flower – that person is in charge of the flower ( three people with 1 petal, one person with a flower).
  5. Flower pupils form a group and start sticking their flowers together.
  6. Petal pupils work with new people in groups of 5 and create another flower.
  7. Eventually 12 flowers are completed and stuck together.

 

Notes:

  • String should be firmly attached before the ball is complete.
  • It is advisable to staple a half ball to card or the wall to prevent it collapsing.

 

Thank you to @c0mplexnumber for the original inspiration for this activity.

Have fun folks!