This student really knows how to make eye-catching notes.
There was even a key:
344. Picture of the day
Leave a reply
Category Archives: General
343. Butterflies, dreams and stories: How to say goodbye
It’s finally here. My Y11 form group are going on study leave next week. I’ve been their tutor since the summer of Y8. They really are a lovely bunch of students. I’ve been planning their goodbye for some time.
Dreams
Since Year 9 I’ve periodically given out “100 things I want to do with my life” sheets. I found the image on Pinterest. They’ve added their aspirations over the years. Some are more detailed than others, depending how seriously they took it.
Butterflies
Inspired by the origami of Clarissa Grandi and her amazing website, at the start of Year 10 each student made a butterfly. Each student wrote a hope or dream or positive message on a coloured luggage tag. They attached the luggage tag to their butterfly and I put them up on the wall. They’ve been there ever since.
Stories
I wrote a silly story with every students’ name included. Some are obvious, some are sneaky.
Finally
I put each ‘bucket list’ back to back with the story, then laminated them (if students want to add to their lists they can just use a permanent markers). Each laminated sheet was rolled up and secured with a cheap hair elastic. I then slipped the luggage tag under the band. They look like graduation scrolls.
All these things could be done in a much shorter period of time. I think they will be a personalised memory of their time at school.
342. Revision jotters
With the exams looming large, I thought I’d share how my class have been revising. To give you some context roughly a third of the class are doing Foundation GCSE, aiming for at least a Grade 4. The rest are doing Higher and aiming for a Grade 5 or better. We have three, one hour, lessons a week. I’m rotating between doing an exam paper, a whole class revision activity (eg a revision clock) and tiered revision.
I know if I tell the students to revise independently the results are going to be mixed. Some will be brilliant, some will be more laid back. To resolve this I pick a topic (or two) from each tier that I know they need to improve on from or that they have requested. It’s helpful if there is a theme to the work. I’ve recently done things like y=mx+c (F) with plotting inequalities (H).
Now the genius part: PixiMaths revision jotters
How to run the session
Photocopy a big stack of revision jotters. If you are doing black and white copying, use the b&w version. We requested the b&w version and, because PixiMaths is awesome, it is now on the website.
Clearly put on the board which topic each tier is revising
Eg Foundation: exact trig values, Higher: trig graphs
Give students 5-10 minutes to fill their revision jotters with everything they know. Have textbooks or maths dictionaries available to fill in the gaps. You may find that Higher students want to do the Foundation topic too – no problem, just make sure they have two jotters. Due to the complexity of the Higher topic, they will need more time to make initial notes.
My students are allowed headphones in revision sessions. At this point it’s headphones in for Higher and out for Foundation.
Do a skills recap on the board (exact trig values), with maybe an exam question too. Students can ask questions on the topic and add to their jotter. Then have a worksheet for students to do eg Corbett Maths or KeshMaths GCSE exam questions booklets. They can refer to their revision jotter or scan the Corbett Maths QR code for extra help.
Swap over. Headphones in for Foundation and out for Higher.
Repeat the process for Higher, with drawing trigonometric graphs. Issue an appropriate worksheet.
Once you’re done, make a judgement call. Are there students who could push it further? Maybe transform a trig graph or problem solve? Go for it. Foundation are busy, Higher are busy, spend some time stretching your most able. Every mark counts.
A huge thank you to PixiMaths for the revision jotters (and everything else).
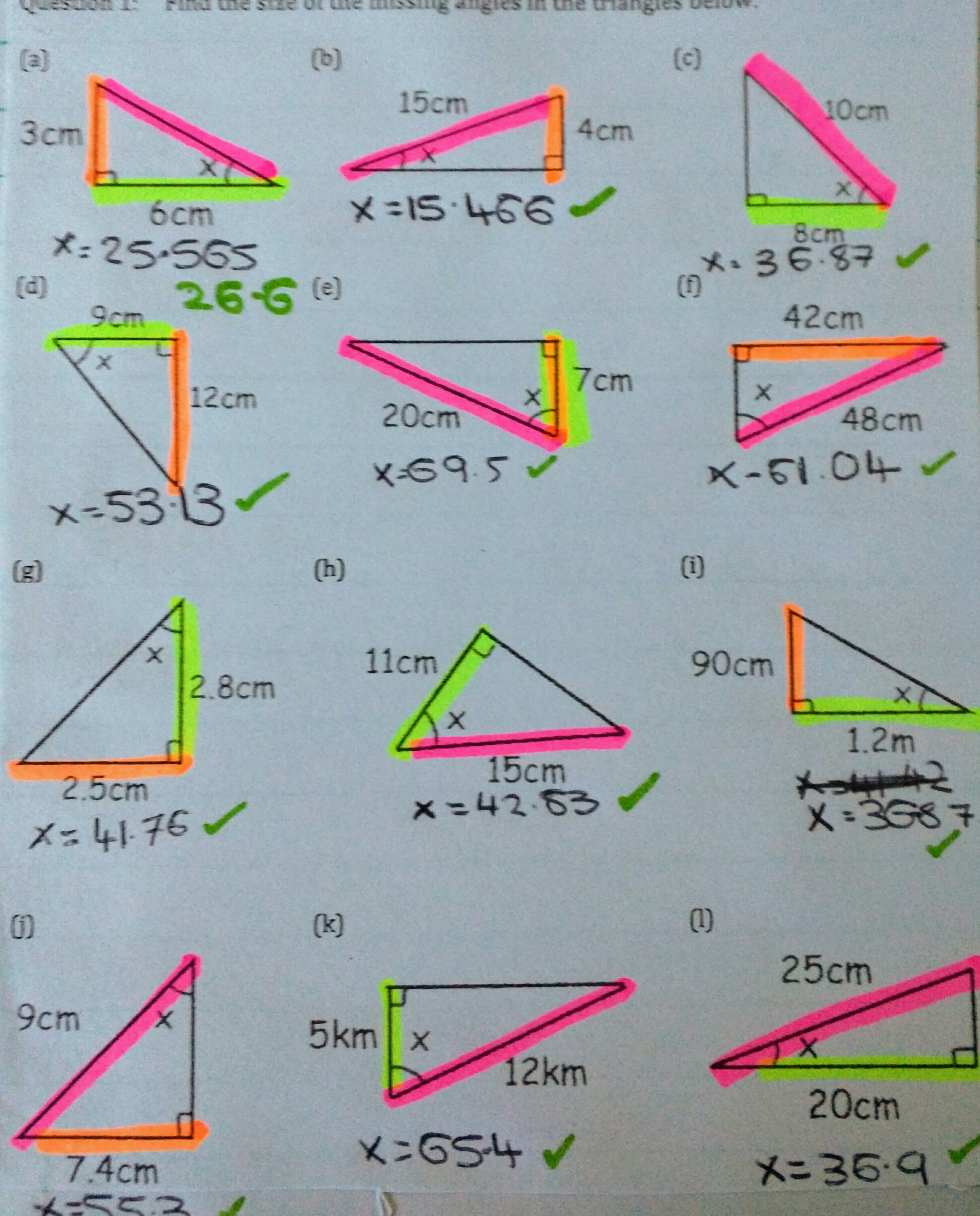
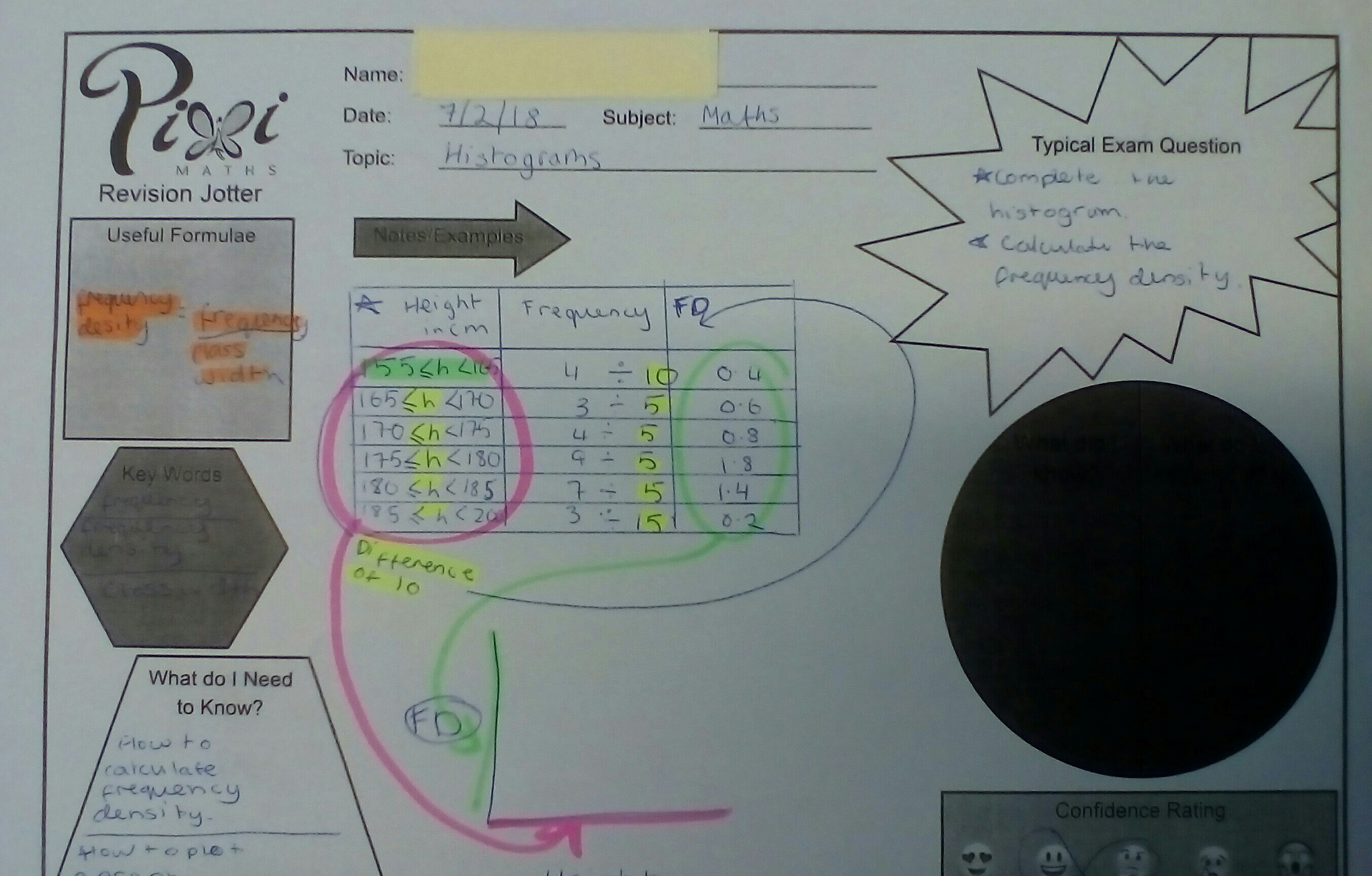
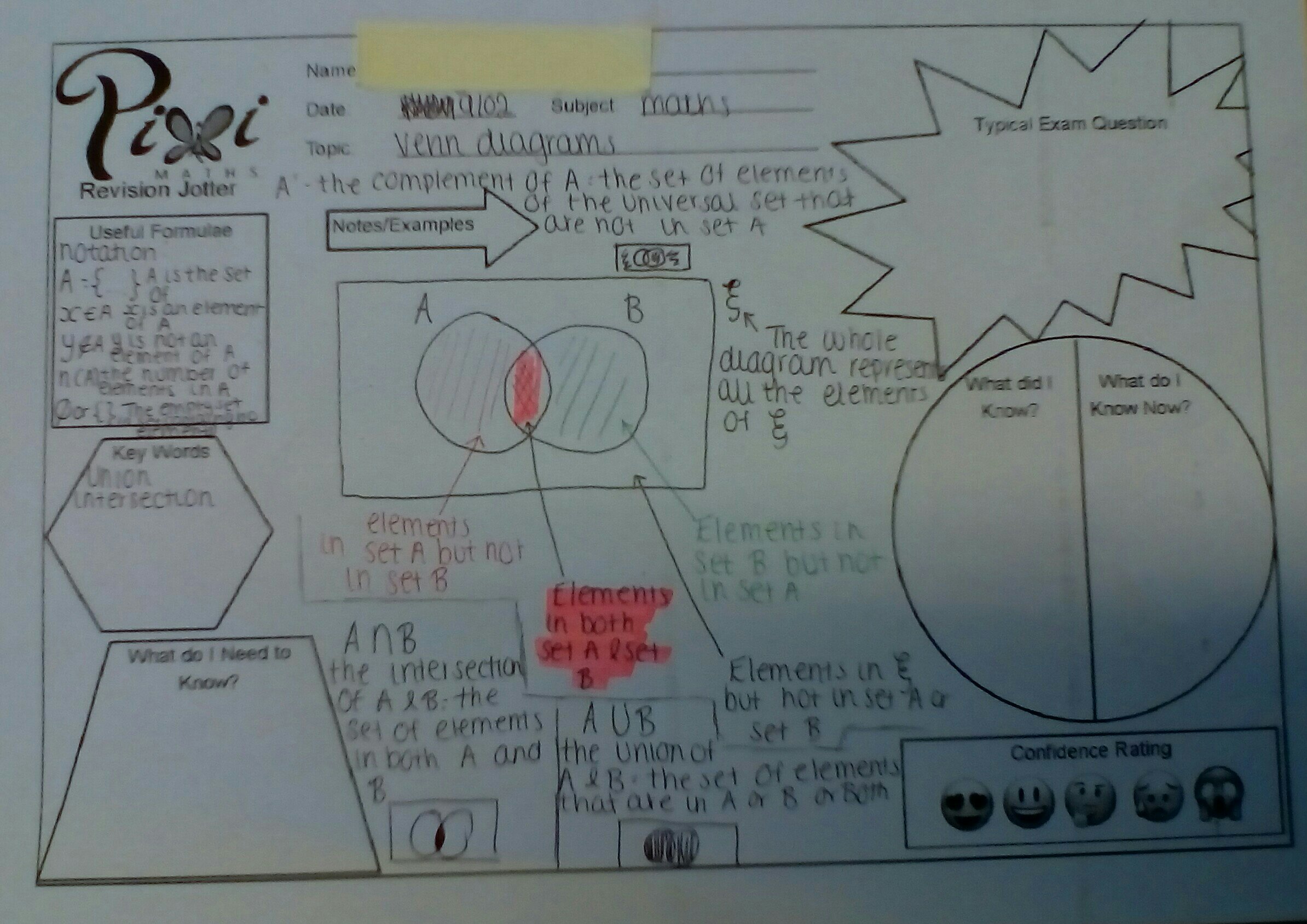
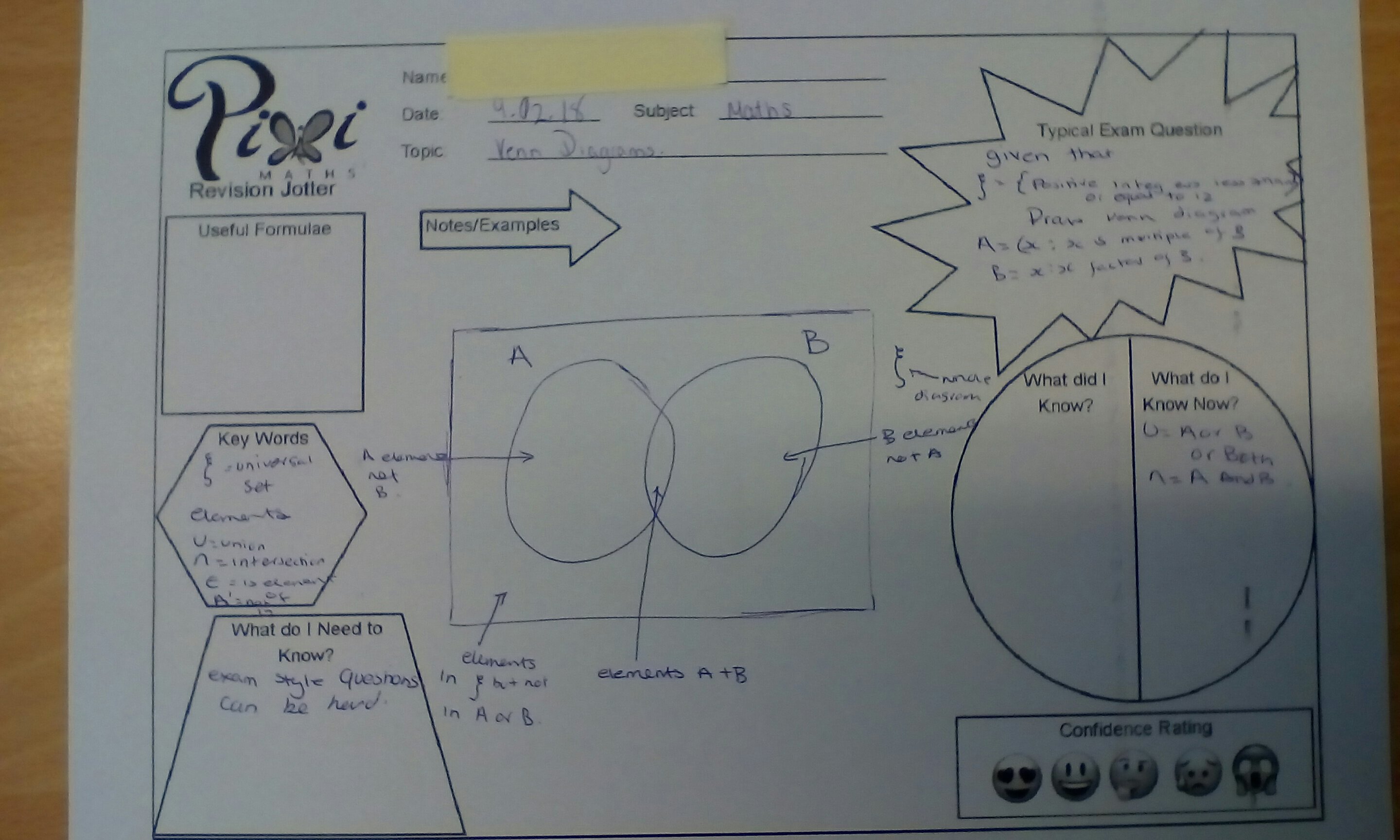
Examples of students’ work
Shared with permission of students. You can see that they have personalised them to meet their needs and some are a work in progress. Also, the b&w jotter photocopies so nicely.
341. Dragon Bridge
Here is a little starter picture for you:
This is the ‘Pont y Ddraig’ at the marina in Rhyl, in North Wales. What mathematical questions could be inspired by this?
‘Pont y Ddraig’ means Dragon Bridge. Find out more about the bridge here
339. Broken rotation
This is a quick post following a discussion in the office today. The prompt was a colleague asking “How do you teach rotation to a child with two broken arms?”
The last ‘child’ I taught with two broken arms was a sixth former and it involved profuse photocopying of notes.
But back to the problem. You could cut out shapes and rotate them on a gridded whiteboard. The student could get a feel for what was going on and be part of the whiteboard Q& A session. For the main classwork, photocopy the worksheet or textbook and increase it to A3. Make a second colour copy and cut out the shapes in the questions. The student can then move these into the correct places to answer the questions. The work could then be photographed, emailled to the teacher or printed out.
Of course I do mean use a phone to take a picture, because it’ll take more than two broken arms to stop a teenager using their mobile phone.
(BTW I’m not making light of the student’s problem. It’s important we think around these issues to ensure all students can access the curriculum)
337. Surreal symmetry
I stumbled across this splendid website and Instagram feed through an article in ‘The Guardian’ newspaper:
Accidentally Wes Anderson
The site owner has collected together images of buildings that look like they could be in a Wes Anderson film.
Image Credit: #accidentallywesanderson
The result is a stunning collection of images of symmetrical architecture from around the world. The photos could be used as a starting point for a discussion on symmetry, shape or the mathematics of the world around us.
336. Geometry Snacks
If you are looking for a very last minute gift for that special Mathematician in your life, or you have Christmas money to spend, may I recommend “Geometry Snacks” by Ed Southall (@solvemymaths) and Vincent Pantaloni (@panlepan)?
It is a nearly pocket sized book of geometry puzzles whose construct of simple, elegant problems can decieve the unwary into thinking the solutions are easy. This is a book for those who embrace mathematical rigour, rather than repetitious guesswork.
In fact, forget buying it for someone else – get one just for yourself!
Geometry Snacks is published by Tarquin (ISBN: 9 781911 093701)