To an experienced mathematician, factorising a quadratic (with real roots) is a little number puzzle, into which the algebraic terms fall gently into place.
To a secondary (high) school student of middling ability they can be algebraic torments conjured from the darkest recesses of a fevered genius’ imagination. Impossible!
This year I have introduced factorising with no mention of algebra, equations, solving or factorising. My class are at least C grade students who have convinced themselves they are no good at algebra. We started by considering this puzzle:
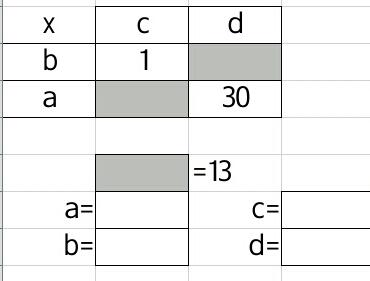
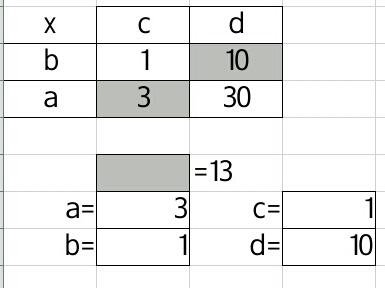
What values of a, b, c &d make this multiplication grid true?
bc = 1
ad = 30
ac + bd = 13
The solution is fairly straightforward:
Once they got the hang of this kind of puzzle, I compared it to the grid method for expanding double brackets. I asked them to think about what the brackets could be if I gave them the values for bc, bd, ac & ad.
Finally the stabilisers were taken off. I asked them what the brackets were if I gave an algebraic form of the number puzzle. First we considered:
bc = X squared co-efficient
ac + bd = X co-efficient
ad = constant
Once it clicked that this was just a fancy number puzzle they were flying. I was really impressed by their positive attitude and willingness to try.
You can download a set of questions (and answers) here.

Pingback: #mathsTLP 26th April 2015 | Solve My Maths
Pingback: Factorising Quadratics (TLP) | Solve My Maths