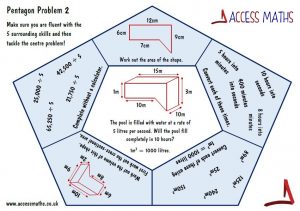
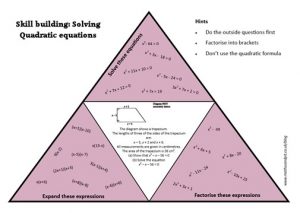
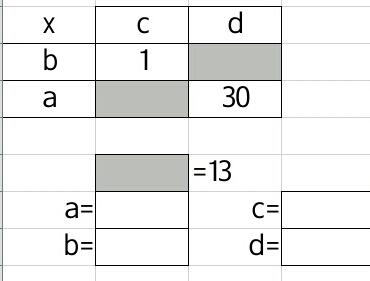
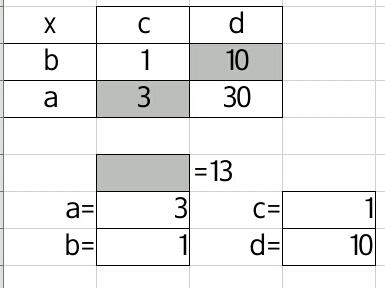
Back in posts 95. Quadratic puzzles and 322. Quadratic puzzles I’ve looked at how to approach factorising and solving quadratic equations/expressions in a ‘gentle’ way.
Time to take off the kid gloves!
I have an awesome class of 13 year olds who are starting out on quadratic manipulation. They are great, but there are a significant number who rush their work and skip steps of working out because they ‘know what they are doing’. Really? Let’s see …
I gave the class twelve quadratic expressions and asked them to factorise them, then to spot any common themes. What I didn’t tell them was that all of the factors used were combinations of x, 2x, +/-1 and +/-5. If they were sloppy with their attention to detail, their solution would look like the solution to a different expression. Essentially a difficult easy task.
It soon sorted out those who had at true understanding of factorising a quadratic from those who’d lucked their way through easier questions.
I’ve shared the presentation and pdf version below. I’ve added in two slides where you can cut out the expressions to use as more of a card sort. You’ll notice that there are no 4x^2 expressions – I was focussing on solutions with only one x co-efficient greater than one. Although I used this as a starter, you may wish to use it as a longer activity, depending on your class.