Answer:
If this is your crop on your farm!
This is center pivot (or central pivot or circle) irrigation. The area which is watered is pretty obvious. There are plenty of images on the internet and sites full of statistics.
I could imagine this making a good research homework. Apart from simply working out the fertile area, you could look at volume of water used – you could even work out the optimum size and number of circles for maximum coverage!
So, you’ve got term to term sequences sussed. Time to tackle Nth term!
This idea just sort of appeared in my sequences lesson.
Equipment
Giant playing cards (or numbers on two different colours of A5 card)
Numbered headbands (I made crowns out of corrugated border card)
Set Up
1.Lay out one coloured set of cards on a table or the floor – these are the ones we needed in class. We started with all the cards in the suit.
2. Issue headbands to four pupils.
3. Pupils stand in number order.
4. Give each pupil a different. coloured card from a sequence to hold facing them.
Task
1. Explain that each person represents a term in a sequence, given by the headband.
2. Pupil 1 turns around their card – Red 3.
Question: What is the next number?
Answer: Don’t know
3. Pupil 2 turns around their card – Red 5.
Question: What is the next number?
Answer: Might predict 7
4. Pupil 3 turns around their card – Red 7.
Question: What is the next number? Why?
Answer: 9, add 2.
5. Reveal the last number – Red 9.
6. What is the pattern? Add 2 Which multiplication table has the same pattern? Twos
7. Give each pupil in the sequence the appropriate number from the two times table.
Question: How do you turn the two times table into the sequence?
Answer: Add 1
8. How do you get from the headband to the sequence?
Headband x 2 + 1 = sequence
9. What about a headband with 10 on it? Or 100? Or a mystery number?
10. Try this with other sequences and develop the idea of Nth term.
Outcome
I used this as a plenary for a term to term sequences lesson with a shared class. In the following lesson my colleague, D, used this idea to develop the concept of Nth term with another class. He wanted to make something for the pupils to have in their book to remember this. This is what he came up with: Handout for sequences intro (pptx) or How to for sequences(docx). I’m currently trying out hosting my own resources, rather than using TES resources – so we’ll see how effective this is.
So many people have the preconcieved notion that there is only one right answer to a maths question. This is such a silly idea – they just haven’t had the right question!
Here is a simple starter for introducing term to term sequences.
Equipment
Classroom whiteboard or large sheets of paper
Imagination
Task
Write down the next three terms in the sequence 1, 2 … and the rule used.
Eg: 1, 2, 3, 4, 5, … Add 1
Note: Rules should be one short sentence.
Outcome
My Year 7 were frustrated that I’d given them the obvious answer and was asking for more. After a few minutes adjusting their expectations, they went for it. Some methodically wrote down rules, some abbreviated rules to symbols, some wrote rules and didn’t check them. Some didn’t write rules at all.
I randomly picked pupils to share their ideas on the board. I did the writing as I wanted to control the wording of rules and half of them can’t reach the top of the board.
Their sequences were brilliant and very creative. The stumbling block was the rules. They didn’t always work for every term of the sequence. This gave other pupils the opportunity to develop their ideas by improving or adjusting the rules to fit the sequences. We also discussed how many terms you need to make a unique sequence. By the end of the discussion we only had one sequence without a rule. I was really impressed by their numerical skills!
In the subsequent classwork, their solutions were precise and well explained.
We finished with this brain teaser:
1,2,5,10,20,50,100 …
It’s UK currency:
1p,2p,5p,10p … etc
As promised, I’ve been trying out ideas from TeachMeet North West at Calderstones School. Here’s the first post:
My colleague J had mentioned Discovery Puzzlemaker last term, but I’d not had time to try it out. Then Fiona Bate @fibate used it as part of her presentation on ‘Profound thinking in the classroom’.
How I used Puzzlemaker
I decided to test this out on my Year 9 students – they are a bright bunch and there are a lot of them. I put out tile puzzles on sheets of A5 and the class settled to the starter task, after they’d got their books out. There were lots of different strategies and eventually everyone cracked the code – the formula for the area of a circle.
Blank puzzle
Different strategies
The funniest part was later in the lesson. A student put his hand up and said he couldn’t remember the rule for the area of a circle. More than one of his peers pointed out he’d just spent ten minutes cracking a code where the rule was given and it was still on his desk in front of him!
Lesson Objectives
Luke O’Hanlon @funkwalkee did a presentation on ‘Ways to engage with Learning Objectives’. This linked nicely with using Puzzlemaker to discover the aim of the lesson, as well as encourage independent learning and problem solving. Once the class had cracked the code they knew what they’d be doing that day.
Puzzlemaker
As you can see, Discovery Puzzlemaker is a really useful tool. I’m going to use some of the larger puzzles as homework tasks for my lower ability classes as I can tailor them to their specific needs. I’m starting with the ‘Hidden Message’ task to reinforce circle vocabulary.
Thank you to J, Fiona and Luke for sharing this site/their ideas.
This weekend I was at TeachMeet NorthWest at Calderstones School in Liverpool. A TeachMeet is a free event where anyone can present so long as it’s relevant to education and only lasts 5 minutes.
It was the first TM I’ve been to and I also presented. I’m not sure if anyone understood the opening line of ‘S’mae, dw i’n hoffi deinosoriaid’ (Hi, I like dinosaurs) but at least I did my best for languages day as a Maths ASTosaurus*.
Reflecting on the whole event, I can safely say that it was the most energising CPD event I’ve ever attended. You could never run such a diverse event as a fee paying course. The element of the unknown, not knowing what the next topic would be, kept everyone engaged. The pace didn’t let up – there was no time to get bored or doodle on handouts. By the time I got home, my colleague J and myself had already discussed half a dozen ideas we would implement and come up with a Departmental project that would be good for both our Performance Management and whole school BLP focus.
So, I’m taking a week out of blogging to try out all these amazing ideas that are buzzing around my head. Then I’ll share who the brains are behind the ideas (so you can follow them on Twitter) and the impact they’ve had.
* I describe myself as an ASTosaurus as the AST grade was abolished nationally this year. There are still ASTs, but most are being moved to Lead Practitioner roles.
For those who don’t know, an AST is an Advanced Skills Teacher. To become one, you must prove yourself to be outstanding in all areas and pass an assessment. Unlike Excellent teachers and Lead Practitioners, ASTs can only be assessed by an assessment body from London. Less than 5% of teachers are ASTs and now we are going the way of the dinosaurs.
Cold calling is the infuriating practice of randomly contacting people in order to sell something that they don’t want and didn’t ask for. Don’t ask me for my opinion on this business idea!
Cold questioning is the practice of putting a random question on the board and asking pupils to solve it.
Example: GCSE revision
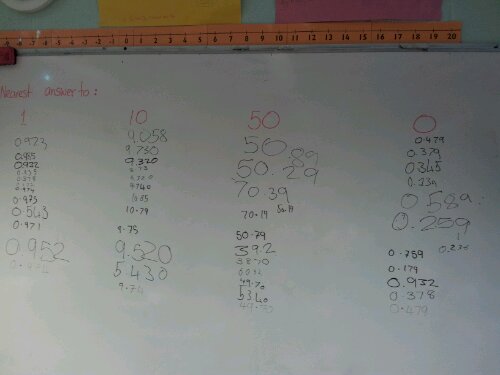
I have a class of critical C/D students who are sitting their GCSE in November. We have been revising prime factorisation, indices, simplifying, standard form and HCF/LCM. Today I put this question on the board:
A pair of trainers are reduced by 30%. The sale cost is £75, how much were they originally, to the nearest £1?
I was pleased to see them talk about the problem and have a go.
Students were randomly selected to share their answers and only two answers occurred – both of them wrong, but with a hint of understanding. Answer A resulted from calculating 30% of £75 and adding it on. Answer B resulted from subtracting the 30% from £75.
Now this isn’t as depressing as you may think, because as we discussed this it became evident that the class were confident calculating simple percentages – they just struggled to apply this knowledge. One student said they had used a multiplier. This opened up the task as we developed the link between reverse percentages and multipliers. Some of the class weren’t convinced, so we had a quick ‘converting percentages to multipliers, including inc/dec’ quiz. We even extended it to fraction to decimal conversion.
Finally, we looked at rounding as it was specified in the original question.
Review
I could have prepared a step-by-step revision lesson, gently taking them through these topics. I think ‘ambushing’ the class with a topic they haven’t studied for a while was more effective as they used a variety of skills to solve the problem, rather than repeat given procedures.
Ambushing your class
*Pick a topic you haven’t looked at for a while
*Avoid easy/obvious questions
*Try to include more than one skill
*Allow sufficient thinking/discussing time
*Finish off with another question, which requires similar skills
(Eg my second question was a reverse percentage involving an increase)
Here’s a mini-investigation on ordering decimals, suitable for Year 6/7 (maybe even Y5 too)!
Equipment
Exercise book (or equivalent)
Pen/pencil
Felt tip pen
Sheet of paper: A4 or A5
Scissors
Activity
1. Fold the paper into 8 and cut along the fold lines. This will give you some spares, just in case.
2. Clearly write 0 and a decimal point onto two pieces with felt tip pen.
3. Choose two different digits and write them down – you now have four activity cards.
4a. What is the biggest number you can make? Arrange it on the desk. (The decimal point can’t be at the end of the number)
4b. Discuss what you notice about the digits and size.
5a. What is the smallest number you can make? Arrange it on the desk (The decimal point can’t be at the start of the number).
5b. Discuss what you notice.
6. What other numbers can you make? There are 12 possible ways to arrange the four cards (according to my class). Encourage the class to be logical and record their answers carefully.
7. Arrange the numbers in order from smallest to biggest.
Activity 2
Add another digit and investigate. My class insist there are 52 possible numbers – I’m waiting for a reasoned justification of this.
What happens if you duplicate a digit?
Follow-up Activity
After completing either activity, ask the class to find the numbers in their lists which are closest to 0, 1, 10 & 50. This helps consolidate their understanding of place value. I asked my class to write their answers on the board. We then discussed the accuracy of their answers.
