On the seventh day of christmas my true love sent to me … seven swans a flipping (through a magazine)!
Image credit: babyanimalzoo.com
Download it here: On the seventh day of Christmas
173. Chrismaths 7
Leave a reply
Tag Archives: wall display
171. Are you ready for ChrisMaths?
I am … well, actually … the noticeboard is nearly ready. Just needs some tinsel and decorations!
This is the title:
You can download it here: Twelve days of ChrisMaths title
This is one of the snowflake placeholders (for Day 3):
The six point snowflakes are quite easy to make :
- Take a square of paper and fold it exactly in half (direction doesn’t matter)
- Mark or pinch halfway along the fold – I’ll refer to it as X
- Put the folded edge on the 0-180 line of a protractor, with X on the centre
- Fold from X along the 60 degree line
- Fold the other end from X to the 120 degree line – you now have 6 equal sections
- Fold the whole thing in half and get snipping
Each of my snowflakes references a number from 1 to 12 and each day the appropriate poster will be put on top of the appropriate snowflake.
164. Plant a Learning Tree
Do you know that feeling when you are starting a topic which is building on existing knowledge and you are not sure how much to recap? Too much recap and they start the topic bored, too little recap and the new work is too difficult. What to do?
To quote an old UK TV ad: “I want to be a tree!” (Prudential, 1989).
I have a bright class of 13/14 year olds and needed to start some algebra work. We ended up making a tree.
Equipment
- Coloured paper
- Felt pens or markers
- Glue
- Scissors
- Roll of backing paper or wallpaper (I cut mine to fit on the back of a door)
- Optional: mini-whiteboards for mindmaps
Activity 1
In small groups, pupils draw mindmaps for the word ‘Algebra’. Encourage them to group or link topics.
Activity 2
Collect the answers on the main board. Any concepts which are not specifically algebra can be categorised as foundation skills eg understand calculating with negative numbers.
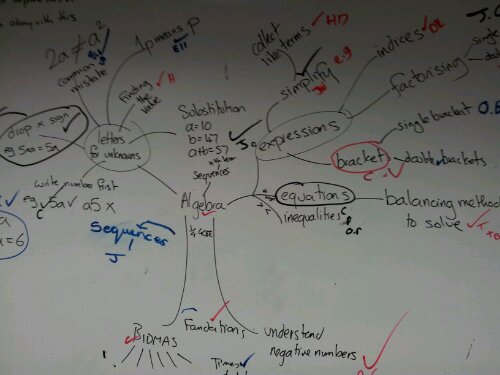
Activity 3
Split the diagram into parts:
Stones: foundation skills which are essential for algebraic success
Branches: subdivisions of algebra
Leaves: specific topics or objectives
Fruit: examples
Activity 4
Assign the different stones, branches, leaves and fruit to pupils to complete.
Activity 5
Assemble your tree. I added an owl and a disembodied voice asking ‘which careers need algebra?’. My branch labels were quickly covered by leaves, so I substituted extra leaves with these labels instead.
Variation
This could work for any topic in any subject. Imagine how good a tree lined corridor would look – a new tree for every area of study.
Review
I moved around the room chatting to pupils as they worked and got a good idea for where I need to start the next lesson. The pupils now have a visual representation of how algebraic concepts link and overlap. In hindsight, I’d probably make the leaves and fruit smaller so that links are clearer.
Show me your learning trees on twitter and I’ll share them on here. @Ms_KMP
138. Kandinsky Combinations!
This week I gave a talk to a group of PGCE/Schools Direct associates about innovation and ‘keeping it fresh’. One of my points was you should ‘Keep the good ideas and bin the rubbish/pointless ones’. This is one of my ideas I kept – first used in the late 1990s!
Background
Wassily Kandinsky was an artist, born in Russia in 1866. He died in France in 1944. He is credited with being the first artist to explore purely abstract work. Researching him is a nice homework task which can add to the final work.
Farbstudie quadrate mit konzentrischen ringen
This work has been reproduced thousands of times -you can see it everywhere from student bedrooms to upmarket coffee shops. The original was completed in 1913. It roughly translates as colour study squares with concentric circles.
Investigation
You will need:
Squared paper (or plain)
Coloured pencils or pens
1. Show the class the painting and discuss how the colours are arranged.
2. How many ways can you colour in one square with one colour? 1
3. How many ways can you colour in two concentric squares with two colours? 2
4. Repeat for three colours and ask for predictions. The usual prediction is 3, the answer is 6.
5. Repeat the process and ask them if they can see a pattern forming. Encourage them to be methodical.
The colour patterns form a set of factorial numbers. Finding out about factorials could be a good extension task.
After the work is completed you’ve potentially got a great wall display, a cross-curricular link to art and an understanding of combinations/factorials.
Variation
This also looks rather cool done with concentric equilateral triangles or hexagons on isometric paper.
126. Kusudama to meet you
Wow … September again and many people will be meeting new faces for the first time. Learning names, setting out classroom rules, figuring out who’s got all the textbooks you need …
Made using origami paper.
Back in July I made Kusudama flower balls with a couple of classes. It occurred to me then what a great ice-breaker they could be. They’d also be a nice maths club project.
Definition of Kusudama from Wikipedia
The Japanese kusudama (薬玉; lit. medicine ball) is a paper model that is usually (although not always) created by sewing multiple identical pyramidal units (usually stylized flowers folded from square paper) together through their points to form a spherical shape. Alternately the individual components may be glued together. Occasionally, a tassel is attached to the bottom for decoration.
Resources
You will need:
- 5 squares of paper for a flower
- 12 flowers for a ball
- 60 squares of paper in total (sugar paper is cheap, but doesn’t tape together well)
- String if you wish to hang it up
- Card if you wish to mount a half ball on the wall
- Sticky stuff: glue sticks or glue dots or pva glue or tape or a hot glue gun – whatever works for you!
- Beads or ribbon for decoration (optional)
Activity
I showed this website to my class: http://www.origami-instructions.com/origami-kusudama-flower.html
It has an instructional video and very clear step by step photographs. It’s so easy a six year old can (and did) do it!
- The instructions assume 30 pupils in a class. Let each pupil make a petal following the step by step instructions and then independently make another (2 petals each).
- Pupils pair up and stick two petals together (1 petal each and 1 pair stuck together).
- Pairs team up with another pair and stick their pairs together (1 petal each and 4 petals stuck together).
- One person in the four uses their extra petal to complete the flower – that person is in charge of the flower ( three people with 1 petal, one person with a flower).
- Flower pupils form a group and start sticking their flowers together.
- Petal pupils work with new people in groups of 5 and create another flower.
- Eventually 12 flowers are completed and stuck together.
Notes:
- String should be firmly attached before the ball is complete.
- It is advisable to staple a half ball to card or the wall to prevent it collapsing.
Thank you to @c0mplexnumber for the original inspiration for this activity.
Have fun folks!
76. Celebrating success
How can you celebrate individual pupils’ achievements, without having different reward schemes for different abilities?
I found this lovely activity at Teachwithme.com. Everytime a pupil achieves a specified goal, their peacock gains another tailfeather. The website has a link to a free pdf template.
You could start a new peacock each term and they’d be a good discussion point at parents’ evening. I also thought you could adapt this for each term: baubles on a christmas tree, leaves on a tree or flowers in a vase.
This would make a very colourful wall display in a Primary or Year 7 classroom and you could adapt it for any subject or pastoral targets.