Category Archives: Number

113. Did the Little Thinkers get you thinking?

1 Reply

Did my Little Thinkers give you ideas for a lesson?

I hope so!

These are my little crisp people and they’ve been helping pupils learn for over a decade.

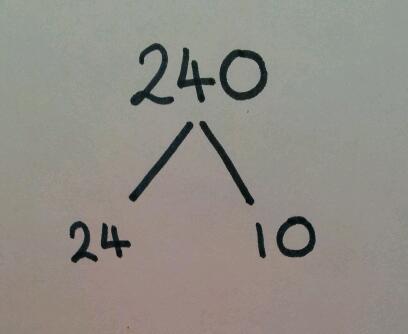
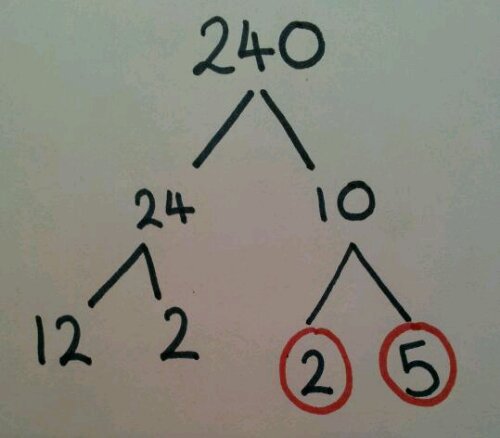
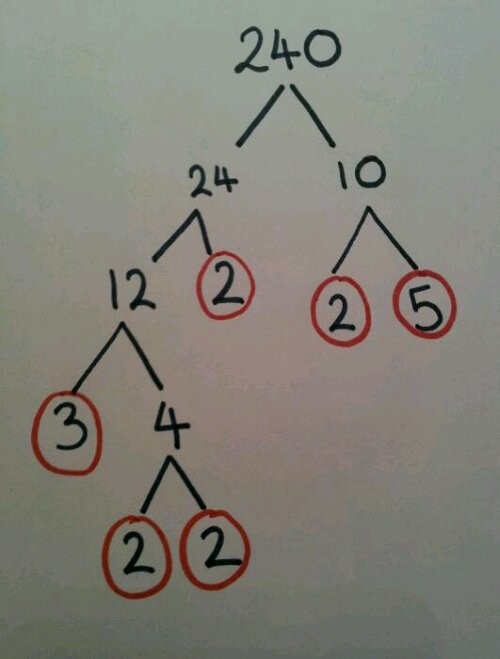
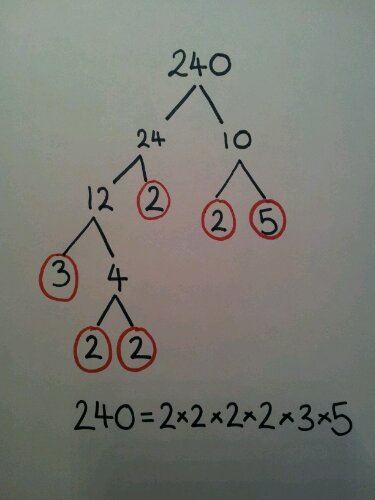
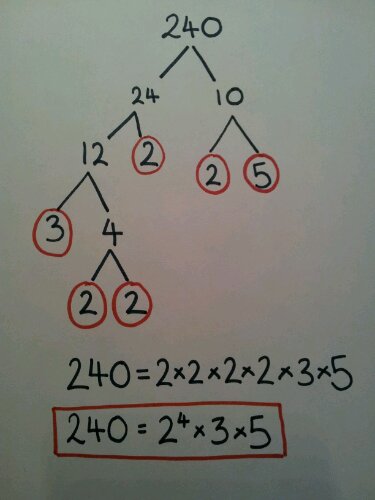
I first thought up this task when an interactive whiteboard and digital projector came in the form of an overhead projector. Using the brand new concept of colour printing onto inkjet OHP transparencies, we could move these little people around the board and investigate different problems. Each number represents the number of bags of crisps eaten in a week. Each colour represents a flavour (Blue = salt & vinegar, red = ready salted, green = cheese & onion, pink = prawn cocktail).

You can sort by number of bags eaten:

image

You can create a flavour pictogram:

image

In fact you can use this resource with KS2 & KS3 to investigate lots of topics:
Sorting by category (number/colour)
Ordering numbers
Pictograms
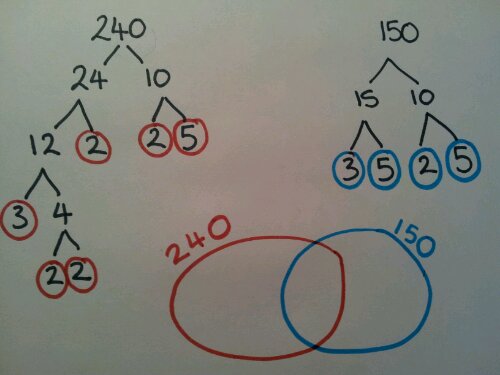
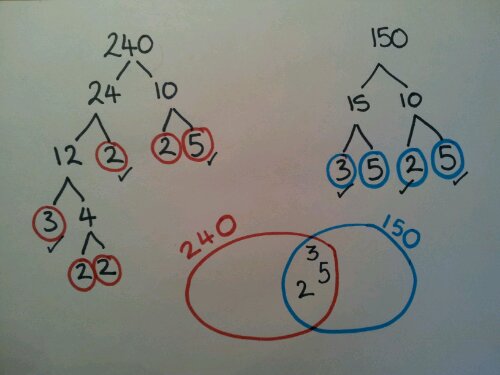
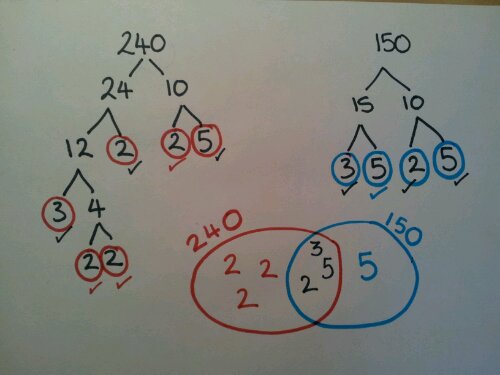
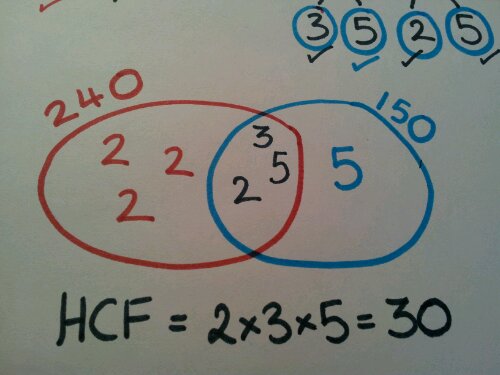
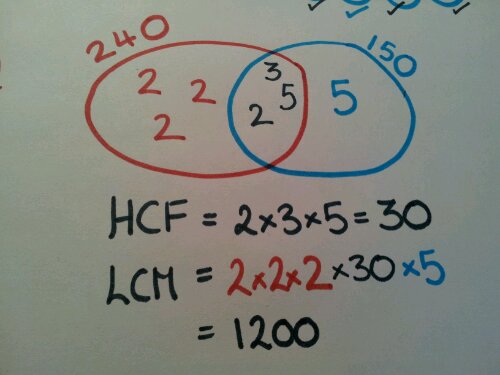
Venn diagrams
Carroll diagrams
Bar-charts
Averages
Questionning
Probability

And anything else you can think of.

I’ve created an editable template of figures, in three different sizes. You print them out and use them individually, in group work or on the wall. There is also a teacher guide on how to use the crisp people.

Enjoy!

Download your little people below:

Editable template  crisp-people-template-blank

Teacher guide and presentation crisp_people_guide

108. Sumlock

Leave a reply

This has got to be my geekiest purchase from an antiques and collectors fayre:

image

It is a working decimal comptometer from the 1960s. To be specific it is a Sumlock model 912/s sterling currency comptometer. It measures 330mm by 315mm by 135mm and was made by the Bell Punch Company. The maximum total it can display is £1,500/17s/11d. This is pre-decimal British currency.

image

I’m fascinated by old maths and science tools and books. I have an old maths instruction pamphlet from the 19th century with a chapter entitled ‘Mathematics for idiots and women’! So this comptometer is just my kind of thing. When my mother-in-law saw it, she told me about their use in offices. She worked with a comptometer operator in the pay office. Comptometer operators had to be specially trained and earned more than your average ‘office girl’.

I’ve been doing some research and found a rather marvellous website: The Vintage Calculator web museum.

The Sumlock Mechanical Calculator page explains all about this machine. It includes pictures of the internal gear mechanism.

There is also a section on ‘Operating a comptometer’. The processes and algorithms that an operator had to learn were quite complicated and they still had to use mental arithmetic – nothing like modern calculators.

I’m sure there is an arithmetic lesson here somewhere…

106. Musical Fractions

3 Replies

Some unbelievers dispute it, but the truth is out there: Mathematics is everywhere!

The link between fractions and music is inescapable. If your notes don’t add up correctly, the music just doesn’t sound right. Crotchets, quavers, semi-breves, time signatures – it’s all maths.

Musical Fractions
I really like doing this activity with Year 7. Please make sure there are no tests or exams going on nearby.

Equipment
Mini-whiteboards
Percussion instruments (or clapping)
Earplugs (optional)

Aim
To introduce and practice adding simple unitary fractions.

Activity
Each type of musical note lasts for a specific amount of time. For example a crotchet lasts one beat. The picture below shows different notes and values:

image

A dotted note lasts 50% longer than it normally would.

Time signatures tell you how many beats are in each bar of music (very simplified explanation). So:
image

To make this into a lesson, ask students to create their own rhythms adding up to 3 or 4 beats.

image

Start by doing 4 single beats by clapping or using instruments. This sounds like ‘tah, tah, tah, tah’ when you say it.

Then try some half notes – one, one, half, half, one. This sounds like ‘tah, tah, ta-te, tah’.

Throw in some quarter notes – one, half, half, quarter, quarter, quarter, quarter, one. This sounds like ‘tah, ta-te, tafi-tifi, tah’.

Now you can let the pupils loose to create their own rhythms using unitary fractions. You can get the pupils to write the fraction additions on their whiteboards. Each group can demonstrate their rhythm and teach it to the rest of the class.

I hope the ringing in your ears fades by the end of the day.

104. Percentages shout out

Leave a reply

I used a great resource from Whidds at TES resources this week:

image

It’s a differentiated percentages trail. You or your students can set the level of difficulty using a neat traffic light system. The resource includes a powerpoint and two different activities.

Download it here.

Thank you to Whidds for sharing this great idea.

102. Can you stay out of the Boardroom?

Leave a reply

The_Apprentice__The_Final

The Apprentice regularly features its contestants failing to listen to what people want, often with disastrous results.

  •  They carry out market research with the wrong people or not enough people.
  • They assume the people they are asking are brilliant or thick. Seriously, you won’t find a world class wine expert working in the local supermarket!
  • They don’t change their product to meet the needs of the people.
  • Worse than that – they ignore the brief!

It all of this leads to one place: The Boardroom

Can your pupils avoid being fired?

I’ve been using ‘The Apprentice’ as an inspiration for a data handling project for years and I’ve finally typed up a resource to go with it.

Download Would Lord Sugar invest in you? worksheet

100. Factor Venn

Leave a reply

In the last post I discussed Prime Factor Decomposition, using factor trees. I also use this method for Highest Common Factor (HCF) and Lowest Common Multiple (LCM). The difference is you need two different coloured pens and a Venn diagram:

Factorise your first number

image

Factorise your second number

image

Draw and label an empty Venn diagram in appropriate colours

image

Fill in the common factors

image

Fill in the rest

image

HCF: Multiply the overlapping area

image

LCM: Multiply everything

image

Review
This method is great for visual learners who want to see where the numbers come from. You can also quickly spot where they have made a mistake in a calculation.

Challenge
This method also works for three numbers – just use three colours and three circles!

99. Factor Races

Leave a reply

I rather like teaching prime factor decomposition as you can assess lots of numerical skills within the topic. I can easily cover:
*Division
*Tests of divisibility
*Multiplication
*Quick recall of multiplication facts
*Prime numbers
*Factor/Multiple misconceptions
*Powers & Index notation
*Venn diagrams*
*Products
*HCF & LCM¤
*Vocabulary related to all the above

Many people already use prime factor trees to teach this topic, but if you are unfamilar with them here is a quick summary:

Find two numbers that multiply to give the top number.

image

Repeat for each branch, circling the prime numbers. These are like the fruit on the end of the branch.

image

Repeat until every branch has ‘fruit’ at the end.

image

Write out the factors, in numerical order, as a multiplication.

image

Collect like factors into index notation.

image

And that’s how to make a prime factor decomposition tree.

The Race
You will need as many pupils as you can standing at your board, all equipped with a whiteboard pen. Depending on which room I am in, I get about 10 pupils out.

Their team mates sit near them – it is up to you as to whether calculators are allowed. Only the person at the board can write.

You call out a number and every team must work out the prime factor decomposition on the board. The winning team is the first to write the number as a product of prime factors.

Teaching Point
Once everyone has completed the task, leave the calculations on the board. You can now ask for comments and corrections. The class should notice that even though the number was split up differently, they all got the same answer. If they didn’t, the class can check for errors.

I like to use this as a plenary or a recap starter. It effectively demonstrates that even though your brain chose to breakdown the calculation differently, you are still correct. This can be a confidence boost to those pupils who think there is only one possible method and don’t ‘get’ that method. Maths is about the strategies and skills to solve problems, not just one approved technique.

¤ To be covered in the next blog post