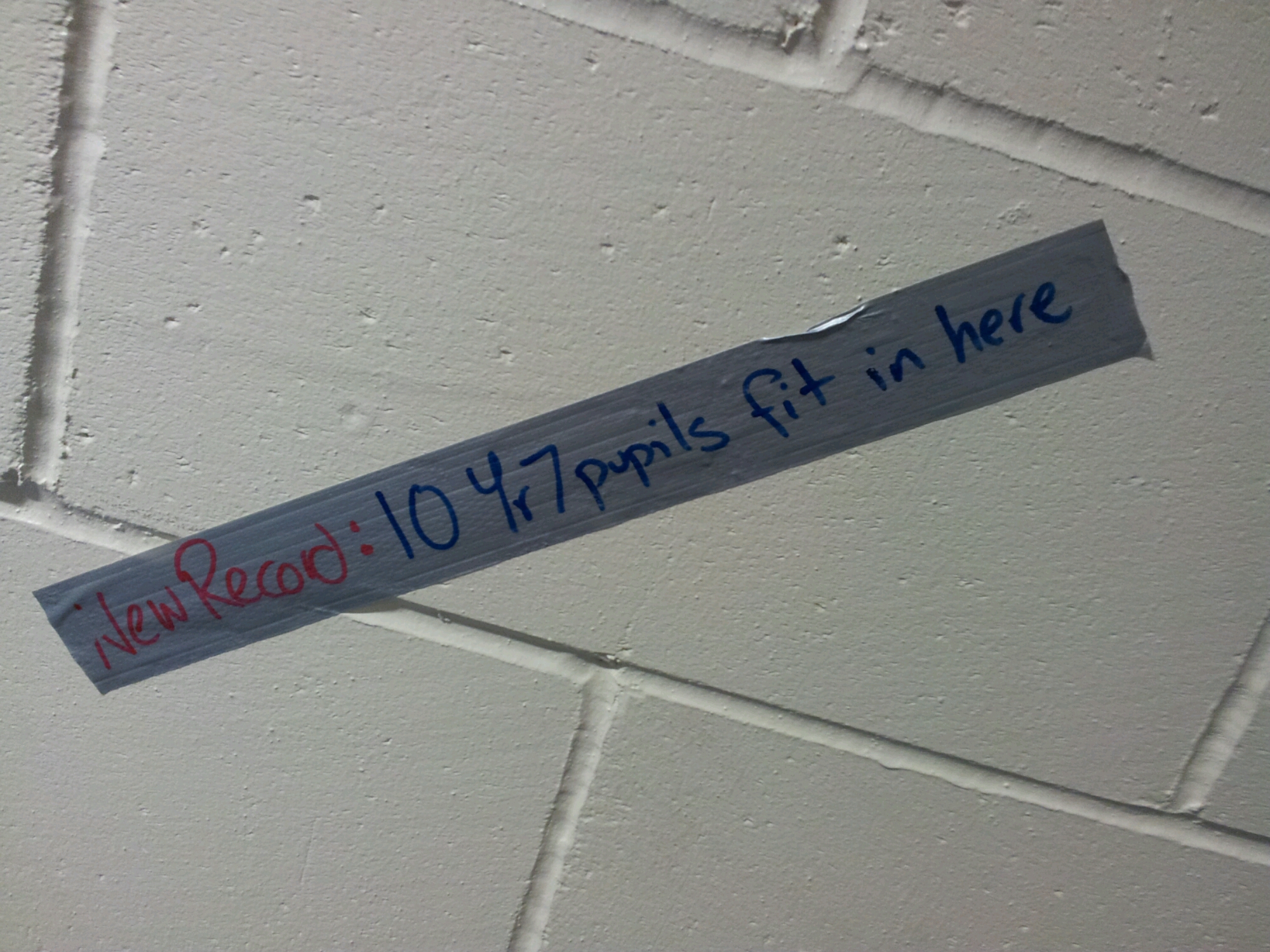Here is a quick cake conundrum for you.
Two girls are decorating the christmas cake. It is a square fruit cake. They share the icing such that one girl ices the top and one face. The other girl ices the remaining three faces. What possible dimensions of the cake will make the icing areas equal?
I spotted this ‘Expert Tip’ whilst flicking through a supermarket magazine:
Image credit: tesco.com/foodandliving
Question
If this cake has a diameter of 18cm (7in), is this a fair way to split it between guests? Can you prove your result in general terms?
Of course, this assumes that the icing on the side doesn’t count in the diameter or guest preference.
I recently came across this splendid resource for introducing Sine and Cosine rule to students.
Proving the Sine and Cosine rule
The proofs for these rules are relatively simple, but getting a class of teenagers to engage with it is a different matter! These worksheets give you the proofs, step by step, but all jumbled up. Students must rearrange the stages in order to create a proof. It worked brilliantly!
Thank you @mrslack_maths
It’s amazing what maths you see when you go for a walk along a canal on a beautiful afternoon. After helping a canal boat through a lock, the following problem occurred to me: how many times must you turn the handle to raise the sluice gate?
Fact: The sluice is controlled by a series of cogs. The handle turns a ratcheted cog with eight teeth.
Fact: The handle turns a small cog with thirteen teeth.
Question: The next cog has ten teeth on a quarter of it’s circumference. How many is this in total?
Fact: This large cog is attached to a small cog with ten teeth, which lifts the vertical post.
Question: From the picture can you estimate how many teeth are on the vertical post?
Question: Given all this information how many turns does the handle need?
Extension: Look at this picture. What is the angle between the foot supports?
Don’t you just hate it when students forget basic key skills? Especially those at the higher end of Year 11 or studying A-Level, who should have a better core knowledge. What if there was a magic tool which began to address this issue?
Skills required
Equipment
You will not need:
Magic Tool
Activity
Quite simply draw the four diagrams below on the board and ask the following questions:
It takes moments to draw the questions on the board, but the discussion can take some time and addresses several basic skills. You can change the numbers to adjust the level of challenge.
Here is a quick fun starter to get your class thinking about dimensions and volume.
Question: How many students can you fit into a metre cube?
The discussion will probably include:
Whilst this is going on make a metre square on the wall and the floor, using duct tape. The inner measurements of the cube are 1m, the rest is just tape border.
The Predictions
Draw up a quick tally chart of how many students they think will fit. A bright child will usually ask how are you going to find out. Easy …
Put students in the cube
Let them put themselves into the confines of the cube. Cue bouncy boys squashing up. Then remind them it can’t be higher than a metre. You might find it useful to have two spare students hold metre sticks vertically at the non-wall end to define the end of the cube.
We managed nine boys, plus gaps at the top for bits of a tenth boy – it wasn’t ethical to chop one up and sprinkle the bits. So we imagined the tenth person balanced on the gaps around their shoulders.
Ten? That is a new record for this activity!
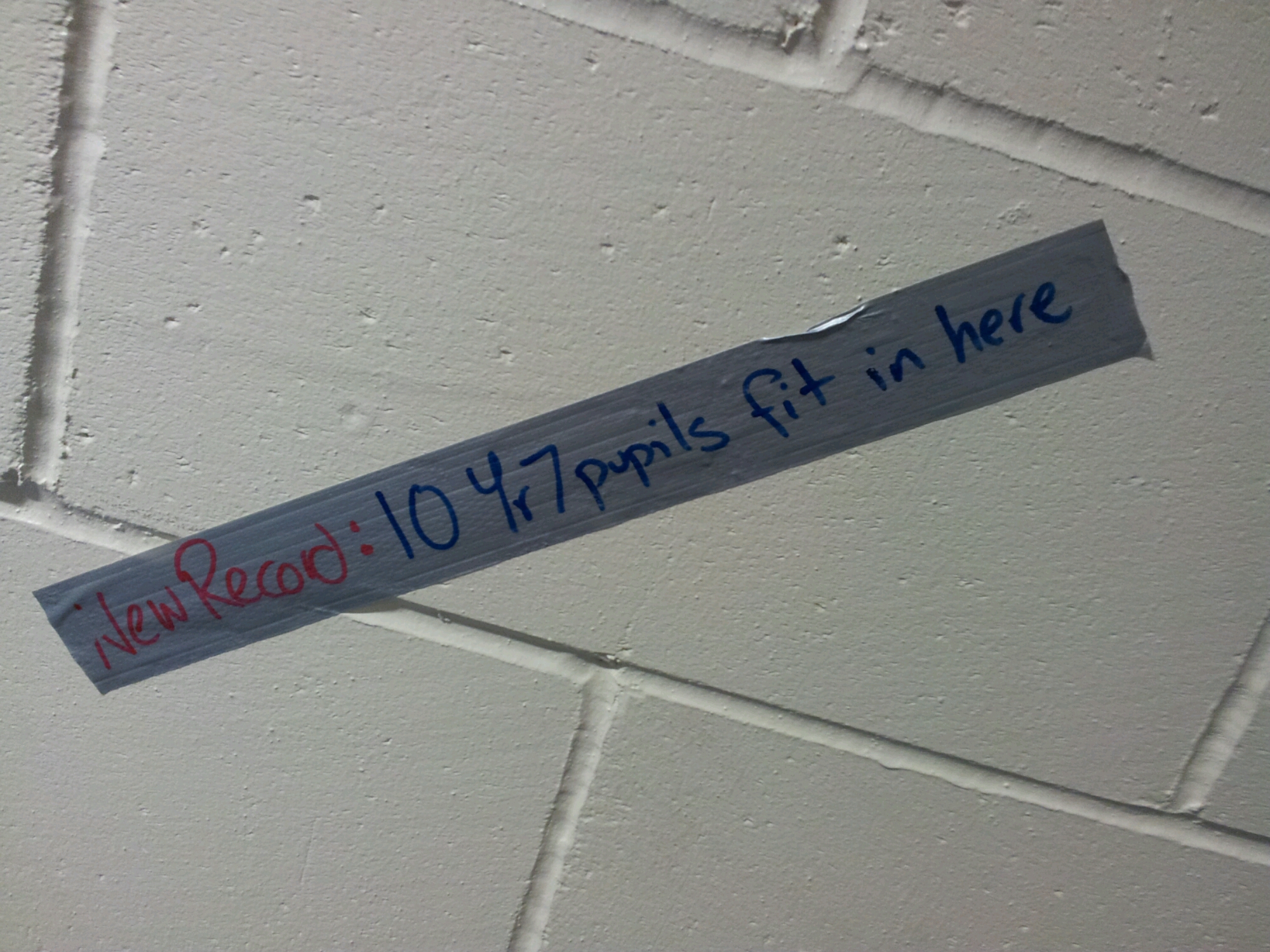
The Point
Even better if …
I’d love to get sturdy board covered in birthday (or Christmas) paper to put under and around the cube to start a discussion about surface area. You could make a big show of unfolding the cube and laying the wrapping out on the floor to form a huge net.
Note
I used to do this by taping metre sticks into a cube, but they fell apart easily. In some schools three metre sticks is a challenge, twelve would be a miracle find. Duct tape works much better!
I like to encourage students to discover rules and formulae for themselves. It’s important that students understand where the maths comes from so they can apply their skills effectively. They also don’t have to rely on remembering a rule (which they may forget when they are stressed).
Image credit: http://www.ck12.org/geometry/Surface-Area-and-Volume-of-Cones/
This resource is a neat and effective way to investigate the surface area of a cone through measuring circles and creating a 3D shape. Students get a physical feel for how the dimensions fit together. Throughout the lesson I let students choose their degree of accuracy in cutting, measuring and calculating. Of course, when we discussed the ‘solution’ at the end of the session it was impossible for me to put one correct answer on the board. So I generalised using a and b for the radii – explaining that everyone could check their method in general terms. The lovely ‘penny drop’ moment happened when my a’s and b’s suddenly became a general rule. I’d conned the class into using algebra because of the accuracy issue.
Download the worksheet and answers here: Surface_area_of_a_cone
Hint: Copying onto coloured paper or card makes this activity stand out in their notes.