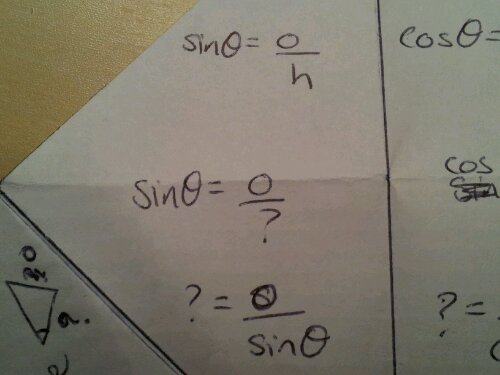This quick activity shows that although the sides change in similar triangles, the angles stay the same. It can also be used with enlargement.
Equipment
Two pieces of different coloured card (A5 or A6 is fine)
Ruler
Pencil
Scissors
Sticky tape
Step by step instructions
Two Lines
Draw a line parallel to the long sides of one piece of card (min 2cm from the edge)
Wrap
Place the two pieces of card at 90 degrees to make a cross.
Wrap the lined card around the unlined card
Cut
Mark out a triangle using the pencil lines as a guide.
Cut along two sides as shown. It’s okay to tidy up a messy cut, so long as the line remains straight.
Stick
Turn over the card and refold in the opposite direction. Stick the bottom edge of the folded card in place, as shown.
Slide
Slot the second piece in place.
Turn over.
As the slider moves up and down a contrasting triangle appears and disappears.
You can measure the sides & angles of every triangle you make.
This can be stuck into books by gluing along the folded edges, which still allows the slider to move.