Tag Archives: problem solving

293. Boxing Bounds

Leave a reply

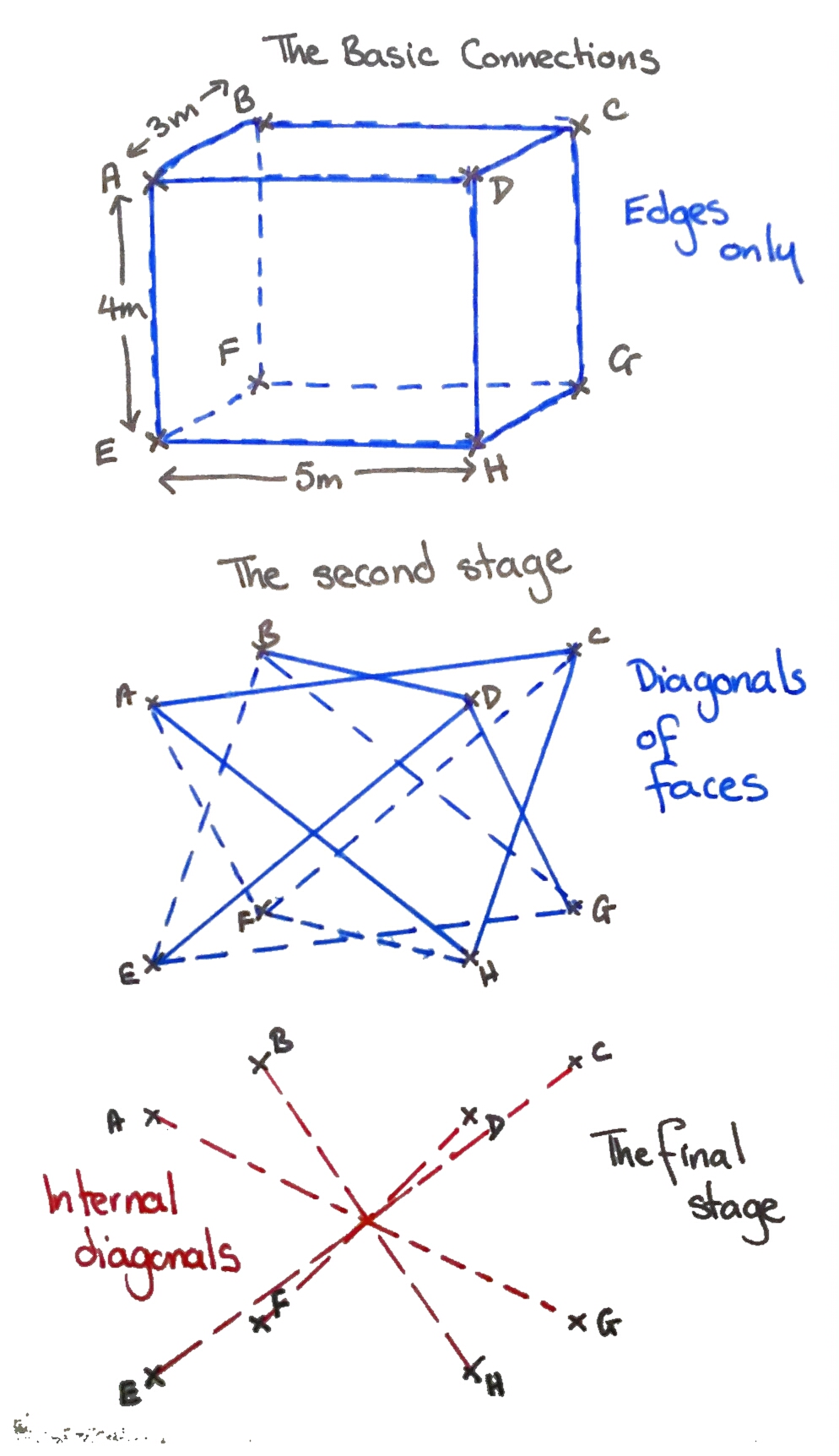
I thought this would make a nice little starter – address a few different topics, bit of problem solving, all over in 15 minutes. How wrong I was!

The Question: A company packs toys into boxes which measure 12cm by 8cm by 10cm (to the nearest centimetre). The boxes are packed into crates which measure 1m by 0.75m by 0.8m (to the nearest centimetre).
(a) Basic question – How many boxes fit into the crate?
(b) What is the maximum volume of a toy box?
(c) What is the minimum volume of the crate?
(d) Look at your answers to (b) and (c) – do they affect your answer to (a)?

It was a simple question about fitting toy boxes into a shipping crate. It extended to looking at upper and lower bounds, then recalculating given this extra information. Simple? No chance!

Problem One
Not changing to the same units

Problem Two
Working out the two volumes and dividing to find the number of toys. When challenged on this, it took a while to get through to the basics of how many toys actually fit – mangled toys and split up boxes don’t sell well.

Problem Three
Maximising the arrangement of boxes – remainders mean empty space

Problem Four
Using the information from Problem Three to find the total number of toys

Problem Five
Working out the dimensions and volume of the empty space in the box

Problem Six
Trying to convert centimetres cubed into metres cubed. I don’t even know why they wanted too!

Problem Seven/Eight
What’s an upper/lower bound?

Problem Nine
What do you mean that the original answer changes when the box size alters?

Problem Ten
All those who weren’t paying attention when you went over Problem Two and don’t ‘get’ why the answer isn’t 625!

268. Monkeying with Pythagoras

Leave a reply

My (not so little) monkeys in KS3 have been discovering and using Pythagoras’ Theorem. They usually deal with open questions quite well, however this one took a fair bit of discussion. This challenge requires no worksheets or fancy resources, just write it on the board. The context is modified, but the essential question remains the same.

Challenge

Zookeepers have attached eight bolts in a cuboid formation (sides 3m, 4m and 5m) to the trees in a chimpanzee enclosure. The keepers attach taut ropes between the bolts for the chimps to climb on. Each length of rope is individually cut. No length is lost in knots.

  • What is the maximum length of any one piece of rope?
  • What is the total amount used, if every corner is joined without duplication?

 

Solution

The first step to solving it is a good diagram of the problem. Students then need to break it down into triangles. The solution has several levels of difficulty:

  • Total of the edges of the cuboid
  • Total of the diagonals on the faces
  • Total of the diagonals across the inside of the cuboid

This diagram demonstrates the levels of the problem – have fun!
image

259. Squashed Tomatoes

Leave a reply

If you taught in England while mathematical coursework still existed, this post may not be new to you. However those who did not may be pleasantly surprised by the simple complexity of ‘Squashed Tomatoes’!

Aim
To investigate a growth pattern, which follows a simple rule.

Equipment

  • Squared paper
  • Coloured pens/pencils
  • Ruler & pencil

Rules
Imagine a warehouse full of crates of tomatoes. One crate in the middle goes rotten. After an hour it infects the neighbouring crates which share one whole crate side. This second generation of rot infects all boxes which share exactly one side. Once a box is rotten it can only infect for an hour, then ceases to affect others. This sounds complicated, but trust me … it’s simple!

Picture Rules

The first box goes rotten – colour in one square to represent the crate. The noughts represent the squares it will infect.

Tomato 1

The second set of crates becomes rotten – use a different colour. The noughts represent what will become rotten next:

tomato 2

The third set of crates becomes rotten – change colour again. At this point it is useful to tell students to keep track of how many crates go rotten after each hour and how many are rotten in total:

tomato 3

The fourth set of crates forms a square:

tomato 4The fifth hour returns the pattern to adding one to each corner:

tomato 5

The sixth hour adds three onto each corner:

tomato 6

Now you can continue this pattern on for as big as your paper is. Students can investigate the rate of growth of rot or the pattern of rot per hour. As the pattern grows, the counting can get tricky. This is when my students started spotting shortcuts. They counted how many new squares were added onto each ‘arm’ and multiplied by number of ‘arms’.

 

Here are some examples of my students work:

image

This is a lovely part-completed diagram:
image

This piece of work includes a table of calculations – you can see the pattern of 1s, 4s and multiples of 12.
image

This is just amazing – you can see that alternate squares are coloured (except for the centre arms).
image

On this large scale you can see the fractal nature of this investigation.

Extension: Does this work for other types of paper? Isometric? Hexagonal?

248. Fair decorations

Leave a reply

Here is a quick cake conundrum for you.

image

Two girls are decorating the christmas cake. It is a square fruit cake. They share the icing such that one girl ices the top and one face. The other girl ices the remaining three faces. What possible dimensions of the cake will make the icing areas equal?

240. Cogged up

Leave a reply

It’s amazing what maths you see when you go for a walk along a canal on a beautiful afternoon. After helping a canal boat through a lock, the following problem occurred to me: how many times must you turn the handle to raise the sluice gate?

Fact: The sluice is controlled by a series of cogs. The handle turns a ratcheted cog with eight teeth.

image

Fact: The handle turns a small cog with thirteen teeth.

image
Question: The next cog has ten teeth on a quarter of it’s circumference. How many is this in total?

image

Fact: This large cog is attached to a small cog with ten teeth, which lifts the vertical post.
image
Question: From the picture can you estimate how many teeth are on the vertical post?

image

Question: Given all this information how many turns does the handle need?
Extension: Look at this picture. What is the angle between the foot supports?
image

236. An Emerald Adventure

Leave a reply

There are assorted holidays coming up and the weather is getting grim. Time to put your feet up and exercise your brain.

Mathematics of Oz

If you like killer Sudokus, logic problems and applied Maths, you’ll love this book. It follows the adventures of Dorothy Gale as she battles her wits against Dr Oz in her journey through the alien world of Oz. The problems are graded so you can work your way up to the harder questions.

You can download a free sample here: Cambridge Press

Buy on Amazon (UK)

I have used problems from this book with all ages of senior school student from able Year 8 to Further Maths A-level students. A word of warning though – check the difficulty level before you let students loose on the problems!

223. Let them eat custard!

Leave a reply

This post isn’t a resource, more of a source of ideas. We tell students that maths is about problem solving, but how many problems are fictitious?
image

Here is a problem, taken directly from ‘real life’ when a friend was making custard on sunday evening.

The question
Do you think the instructions are wrong?
image

Does 2.75 litres of water seem right? Use the whole packet? How much is in the packet?

The problem
image

The custard powder had been bought from the wholesalers. It was such good value because it was a catering pack.

  • If the pack weighs 605g, how much would you need for one portion?
  • How much water would you need?
  • How could you decide if 55ml was a decent size portion?
  • How many pint jugs would the fifty-five 55ml portions fill?

If you have access to a wholesaler or talk nicely to the canteen, you will be surprised how much proportion work you can find in catering size value packs

By the way, my friend did a couple of calculations and a bit of estimating resulting in a large, but tasty, bowl of custard.