Author Archives: MsKMP

148. Ordering Decimals

Leave a reply

Here’s a mini-investigation on ordering decimals, suitable for Year 6/7 (maybe even Y5 too)!

Equipment
Exercise book (or equivalent)
Pen/pencil
Felt tip pen
Sheet of paper: A4 or A5
Scissors

Activity
1. Fold the paper into 8 and cut along the fold lines. This will give you some spares, just in case.
2. Clearly write 0 and a decimal point onto two pieces with felt tip pen.
3. Choose two different digits and write them down – you now have four activity cards.
4a. What is the biggest number you can make? Arrange it on the desk. (The decimal point can’t be at the end of the number)
4b. Discuss what you notice about the digits and size.
5a. What is the smallest number you can make? Arrange it on the desk (The decimal point can’t be at the start of the number).
5b. Discuss what you notice.
6. What other numbers can you make? There are 12 possible ways to arrange the four cards (according to my class). Encourage the class to be logical and record their answers carefully.
7. Arrange the numbers in order from smallest to biggest.

Activity 2
Add another digit and investigate. My class insist there are 52 possible numbers – I’m waiting for a reasoned justification of this.

What happens if you duplicate a digit?

Follow-up Activity
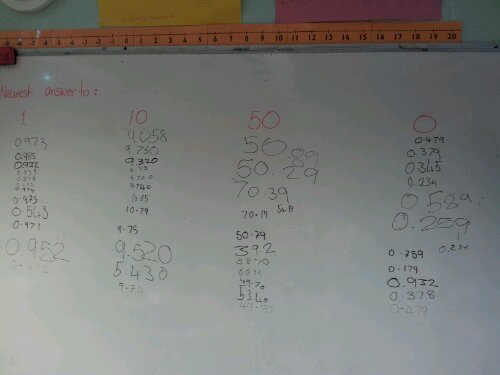
After completing either activity, ask the class to find the numbers in their lists which are closest to 0, 1, 10 & 50. This helps consolidate their understanding of place value. I asked my class to write their answers on the board. We then discussed the accuracy of their answers.

image

147. All hexed up

Leave a reply

So, we all know that regular hexagons tessellate beautifully, but name an example in life that isn’t a honeycomb … takes a bit of thought before you start listing examples.

Here’s a picture to add to your list: the gates at a local playing field.

image

Top detail:

image

Bottom detail:

image

What is more interesting is each hexagon is made from and connected by overlapping S shaped strips of metal. Recreating the structure out of strips of card could be an interesting challenge!

146. Sales Fractions

Leave a reply

A quick idea for you today:

What is the cheapest each item could have been?

image

Which of these is the odd one out?

image

Why is it the odd one out? What discount does it represent? What is this as a decimal or percentage?

Keep your tags the next time you go to the sales – you never know what questions you’ll find.

145. Soroban counts

Leave a reply

I found this really useful book set on a second-hand market stall in the summer. I felt it was worth a look for £3.

image

It is Aba-Conundrums by Evelyn B. Christensen, published by Fat Brain Toy Co. The set includes a soroban, 120 number puzzles (& solutions) on spiral-bound dry-wipe card and dry-wipe pen.

The problem solving elements of the tasks are really good for improving basic number skills.

image

After boring four generations of my family with it, I did a bit of web-searching and came across the Soroban Cymru website – don’t worry if you don’t ‘siarad Cymraeg’, it’s in English.

image

I think proper use of sorobans  could be a really useful tool for developing the understanding of number in low ability Year 6/7. I know they are used by all abilities in Asia, but pupils here don’t generally know how to use a soroban correctly and it could be a way to make numbers more interesting for those who disconnected from maths at a young age. I’m certainly going to try it out this term.

You can get basic sorobans on Amazon from about £2.50.

144. Gadget of the Day 5

Leave a reply

A thing of geeky beauty today:

image

This is a Pocket Decoder for Geocachers, for codebreaking on the go! If you are not into geocaching, it’s still a thing of beauty. The dial is replaceable, meaning you can use it to crack a variety of codes.

Find out more here.

143. Jumping the gap

Leave a reply

The transition from GCSE to A-level Maths is as smooth as can be for some students. Others need the London Underground sign:

image

This time last year the biggest issue (amongst many others) was the lack of logic and rigour in their algebraic solutions and graphs. I tried giving model answers (‘Thank you, Miss’, then file it in the recycling …. Grrr!). I tried explaining why it was important (you could almost hear the shutters slide down in most of their heads). I tried sharing the best student’s work on the board using the visualiser (type of document camera), but all to no avail. The majority of students thought they knew best and ignored all advice.

image

Now rather than go all Professor Umbridge on them*, I switched things around. They critiqued each other’s work.

Activity

1. You will need an exam (style) question, paper and post-it notes.

2. Ask students to complete the question on a sheet of paper – do not write names on it.

3. Put all the solutions out at the front or stick them to the board.

4. Give each student three post-its. They should write something good and something to improve and stick it on the work. Do this three times.

image

5. Each student reclaims their work and reads the notes. They then discuss the feedback and draw up a list of keypoints for improvement.

image

That could be the end of it, but I wanted to remind them of the task so:

6. Collect in the work and notes and mount them on half a noticeboard.

image

7. In the middle of the board put the question, the model solution and their list of key points for improvement.

8. For the next week or so keep referring to the wall display in lesson.

9. Set another question and repeat steps 2-5. Discuss how their work has (hopefully) improved.

10. Fill the remainder of the wall display with the work and comments.

This could be a useful activity to do at the start and end of a topic. It would also be a good BLP (Building Learning Power) activity.

* Professor Umbridge had a particularly sadistic detention task in Harry Potter, where whatever you wrote on the paper was etched into the detainee’s skin. Vile woman, odd ideas on education.

142. Here’s the answer

Leave a reply

I’ve become increasingly interested in an inquiry based approach to learning maths after completing the ‘How to Learn Maths’ course.

Today I tried out a more problem-based approach with a Year 9 class. Last lesson we had recapped prior learning of equivalent fractions, simplifying and multiplying fractions. We had looked at using reciprocals in division. The starter today could easily have been 5 minutes with mini-whiteboards, but instead I gave them to following problem:

image

There is no ‘one correct answer’. The only limit was their mathematical imagination. After about twenty minutes we discussed each other’s answers on the board. If an answer was wrong, it was considered and corrected – rather than being dismissed or ignored. Walking around the room I was amazed – the level of engagement had increased and pupils were explaining their ideas. I could get a feel for who understood and who just followed procedures (and came unstuck when asked to do something different).

Of course, some pupils said ‘I can’t do it!’. They were met with the sympathetic response of ‘Can’t do it, doesn’t work anymore. Challenge is good for you’. Surprisingly, they either got on with it, started working with a friend or asked for pointers on how to start the problem.

I was really impressed with the students’ reaction to the task and by what I learnt about their understanding. Why not try it yourself on your next topic?