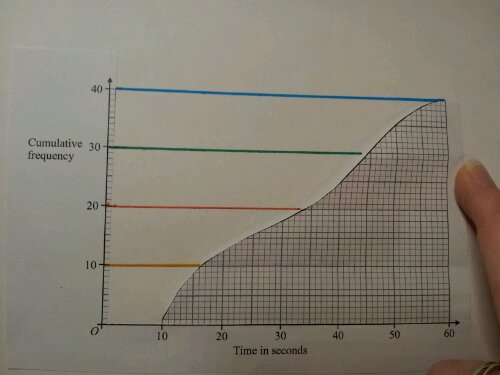
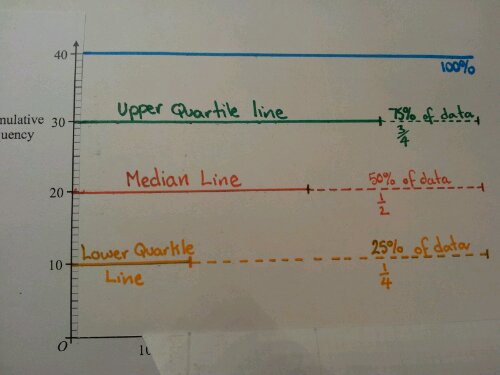
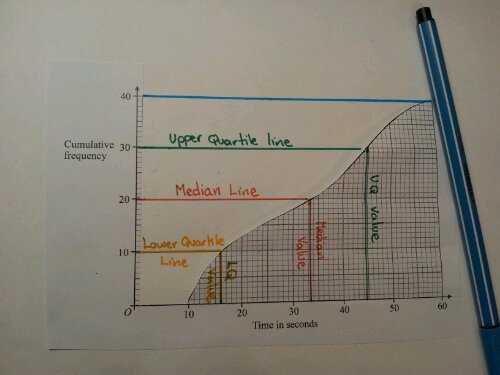
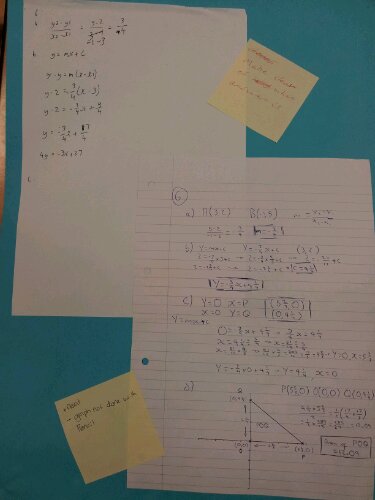Monthly Archives: September 2013

143. Jumping the gap

Leave a reply

The transition from GCSE to A-level Maths is as smooth as can be for some students. Others need the London Underground sign:

image

This time last year the biggest issue (amongst many others) was the lack of logic and rigour in their algebraic solutions and graphs. I tried giving model answers (‘Thank you, Miss’, then file it in the recycling …. Grrr!). I tried explaining why it was important (you could almost hear the shutters slide down in most of their heads). I tried sharing the best student’s work on the board using the visualiser (type of document camera), but all to no avail. The majority of students thought they knew best and ignored all advice.

image

Now rather than go all Professor Umbridge on them*, I switched things around. They critiqued each other’s work.

Activity

1. You will need an exam (style) question, paper and post-it notes.

2. Ask students to complete the question on a sheet of paper – do not write names on it.

3. Put all the solutions out at the front or stick them to the board.

4. Give each student three post-its. They should write something good and something to improve and stick it on the work. Do this three times.

image

5. Each student reclaims their work and reads the notes. They then discuss the feedback and draw up a list of keypoints for improvement.

image

That could be the end of it, but I wanted to remind them of the task so:

6. Collect in the work and notes and mount them on half a noticeboard.

image

7. In the middle of the board put the question, the model solution and their list of key points for improvement.

8. For the next week or so keep referring to the wall display in lesson.

9. Set another question and repeat steps 2-5. Discuss how their work has (hopefully) improved.

10. Fill the remainder of the wall display with the work and comments.

This could be a useful activity to do at the start and end of a topic. It would also be a good BLP (Building Learning Power) activity.

* Professor Umbridge had a particularly sadistic detention task in Harry Potter, where whatever you wrote on the paper was etched into the detainee’s skin. Vile woman, odd ideas on education.

142. Here’s the answer

Leave a reply

I’ve become increasingly interested in an inquiry based approach to learning maths after completing the ‘How to Learn Maths’ course.

Today I tried out a more problem-based approach with a Year 9 class. Last lesson we had recapped prior learning of equivalent fractions, simplifying and multiplying fractions. We had looked at using reciprocals in division. The starter today could easily have been 5 minutes with mini-whiteboards, but instead I gave them to following problem:

image

There is no ‘one correct answer’. The only limit was their mathematical imagination. After about twenty minutes we discussed each other’s answers on the board. If an answer was wrong, it was considered and corrected – rather than being dismissed or ignored. Walking around the room I was amazed – the level of engagement had increased and pupils were explaining their ideas. I could get a feel for who understood and who just followed procedures (and came unstuck when asked to do something different).

Of course, some pupils said ‘I can’t do it!’. They were met with the sympathetic response of ‘Can’t do it, doesn’t work anymore. Challenge is good for you’. Surprisingly, they either got on with it, started working with a friend or asked for pointers on how to start the problem.

I was really impressed with the students’ reaction to the task and by what I learnt about their understanding. Why not try it yourself on your next topic?

141. Book(s) of the week 3

Leave a reply

If you remember ‘The Wonder Years’ you are probably old enough to remember grunge the first time around and television programmes that didn’t involve so called ‘Reality TV’.

image

So what happens to female child stars?

Some have a rocky youth, work really hard and become hugely successful (Drew Barrymore). Some have a rocky youth and become hugely notorious (Lindsay Lohan). Some work really hard, do research, writing and acting, have a theorem named after them and become advocates for women and maths education!

Step forward Danica McKellar!

image

Apart from playing ‘Winnie Cooper’ in ‘The Wonder Years’, Danica is also a successful mathematician. She has written four books aimed at promoting maths to high school students, in particular girls. I strongly suggest you have a look at them or get your school library to purchase them as they are full of inspirational ideas and new ways to think about ‘dusty’ topics.

Her books to date are:

Girls Get Curves: Geometry Takes Shape (2013)

Hot X: Algebra Exposed! (2011)

image

Maths Doesn’t Suck: How to survive year 6 through year 9 maths without losing your mind or breaking a nail (2010)

Kiss my Math: Showing Pre-Algebra who’s boss (2009)

140. Cut out the Quartiles

5 Replies

Quartiles on cumulative frequency graphs are such easy questions when you get ‘it’. The hair pulling, nail biting wrong answers you see on exam papers make you wonder if you’ve ever taught the topic. Time for the scissors again …

Activity
This activity demonstrates in a practical and visual way how to set up the quartiles on a graph.

Equipment
Printed cf graphs
Rulers
Scissors
Glue
Coloured pens

Task
1. Cut out the area to the left of the graph. Leave a column of graph squares next to the y-axis, for scale. Cut exactly to the top of the curve.

image

2. Fold the graph in half, parallel to the x-axis, with the maximum value just touching the axis.

image

Repeat the half fold again
image

3. Fold along the x-axis. Unfold – you’ve just divided the graph into quarters. This should reinforce that y-axis is split into quarters.

image

4. Stick down the axes. Place a ruler on the fold lines and join the ends of the folds to the y-axis.

image

5. If you fold the graph forward you get this:

image

6. Put a mark at the end of each line and continue with a dotted line. Discuss what proportion of the data each line represents and label it.

image

7. Fold the graph back and mark in the vertical lines. Solutions,can now be read from the x-axis.

image

8. The interquartile range can also be highlighted and calculated.

image

Review
This activity covers a fair few learning styles and creates a visual/memorable resource,in their books. Since using it, the number of pupils who quarter the x-axis has dropped significantly. I hope it works for you.

139. Maths Roast

Leave a reply

We’ve all seen the question about using a worded problem to work out the cooking time of a chicken. So dull and in many respects irrelevent – cook books & websites don’t write a big description. This is more like real-life:

Extract from the ‘Reader’s Digest Cookery Year’

image

Butcher’s label – no cooking instructions

image

Equipment
Pictures of labels from fresh meat* (actual labels are a hygiene hazard) – you might want multiple copies
Some cookbooks or tables of temperatures for cooking
Cards saying ‘Delicious’ or ‘Food poisoning!’
Calculators
*Be aware of pupils’ beliefs regarding meat – you don’t want to cause offence

Activity
1. Give out the cooking instructions & labels from the meat, ensuring the actual type of meat is on them.

2. Get pupils to decide how they want to cook their meat. You may also want to specify the cooking method to ensure variety in the,solutions.

3. Pupils calculate the appropriate times.

4. Each person (or group) presents their answer to a group (or the class). The other pupils hold up ‘Delicious’ if they agree or ‘Food poisoning!’ if they disagree. This can lead to a discussion as to why.

5. This can then be extended to look at writing formulae for cooking times.

Vegetarian Option
This task is easily adapted for any vegetarian recipe where weight is important eg Roast squash.

Don’t forget all the work on time and unit conversion that can be included!

138. Kandinsky Combinations!

Leave a reply

This week I gave a talk to a group of PGCE/Schools Direct associates about innovation and ‘keeping it fresh’. One of my points was you should ‘Keep the good ideas and bin the rubbish/pointless ones’. This is one of my ideas I kept – first used in the late 1990s!

Background
Wassily Kandinsky was an artist, born in Russia in 1866. He died in France in 1944. He is credited with being the first artist to explore purely abstract work. Researching him is a nice homework task which can add to the final work.

Farbstudie quadrate mit konzentrischen ringen

image

This work has been reproduced thousands of times -you can see it everywhere from student bedrooms to upmarket coffee shops. The original was completed in 1913. It roughly translates as colour study squares with concentric circles.

Investigation

You will need:
Squared paper (or plain)
Coloured pencils or pens

1. Show the class the painting and discuss how the colours are arranged.

2. How many ways can you colour in one square with one colour? 1

3. How many ways can you colour in two concentric squares with two colours? 2

4. Repeat for three colours and ask for predictions. The usual prediction is 3, the answer is 6.

5. Repeat the process and ask them if they can see a pattern forming. Encourage them to be methodical.

The colour patterns form a set of factorial numbers. Finding out about factorials could be a good extension task.

After the work is completed you’ve potentially got a great wall display, a cross-curricular link to art and an understanding of combinations/factorials.

Variation
This also looks rather cool done with concentric equilateral triangles or hexagons on isometric paper.