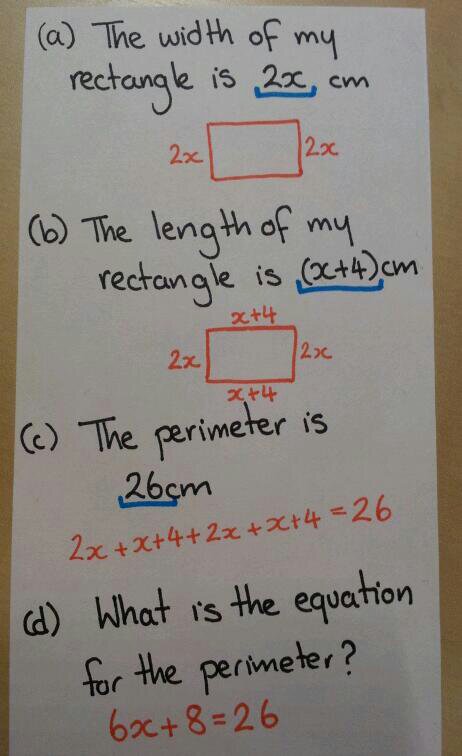
As Mathematicians we appreciate the importance of getting the basics right and building a firm foundation. With this in mind I’ve been an absolute harridan with my Y8 students regarding presentation and technique for solving equations. If they can nail good algebraic presentation now, their future studies will be be much easier.
When we started there were students doing everything in their head, not always correctly. Some insisted on working backwards, which is great for basic cases but not for unknowns on both sides. Most frustratingly some students were breaking up the logic by putting extra working out between steps and losing track of what they were doing.
For example:
2x – 10 = 5x + 8
5x – 2x = 3x
3x – 10 = 8
So we had a really good discussion about logical presentation. We decided to write down what we were doing in the margin, try and keep the = sign lined up in the working and put any extra working out on the right.
This worked really well for most of the class, but I had a small group of students who just lost track of what they were doing and why. They knew things had to balance, but struggled to cope with equations with an unknown on both sides.
While I was talking things over with them using a mini whiteboard, I noticed they had a profusion of coloured pens and highlighters. Bring on the colour!
By highlighting the key point of each line of algebra and matching it with the balancing step they started to build the structure of good solutions. It was slow work to start with, but a couple of lessons later and these same struggling students are now hitting the extension work every time. And most of them no longer feel the need to highlight key information.