This is a quick little post to give you a nifty little resource inspired by the ideas of Bruno Reddy (@MrReddyMaths). I suggest you visit his website at: http://mrreddy.com/.
Image Credit: http://k12math.com/math-concepts/algebra/volumes/volumes.htm
I’ve been teaching my class how to calculate the volume of spheres, cones and pyramids. They really like these staged worksheets. You could print them out as they are, but I personally print them as A5 booklets which fit into their books.
I came across this splendid resource on Similar Triangles, by cturner16, on the TES website:
Similar triangles matching activity
The cards start with a standard diagram of overlapping triangles and you match it up with the individual triangles. The final step is to work out the scale factor and the missing side. It follows the exact steps you would want students to follow when working on these problems.
Now, I know my class well and to avoid the standard bickering, mess and ‘I didn’t think you meant pick up every sheet when you said pick up every sheet’, I copied every set on a different colour:
The colour made it so much easier to manage and discuss. There are six problems, so if your students work in 2’s or 3’s, they each get 3 or 2 sets to stick in their book. The problems are full of misconceptions and interesting scale factors. I’m really glad I used it!
Thank you cturner16!
Speed Cameras are so last century: discerning law enforcement agencies favour the Average Speed Camera!
These motorway delights timestamp when you go through certain checkpoints and calculate your speed between them. No complicated laser guns required, just number plate recognition and a little distance/time calculation. This already sounds like a KS3/4 class activity or a Mechanics A-Level starter.
Equipment
Squared paper
Pencil
Ruler
Coloured pens
Calculator (optional)
Question
Can you find three different (safe) strategies for staying on the right side of the law through extended roadworks? You must average 40mph over 12 miles (original speed limit 60mph).
Visual Prompt
To start off with just draw out blank axes and discuss how you could visually represent this problem.
Idea 1
A distance-time graph
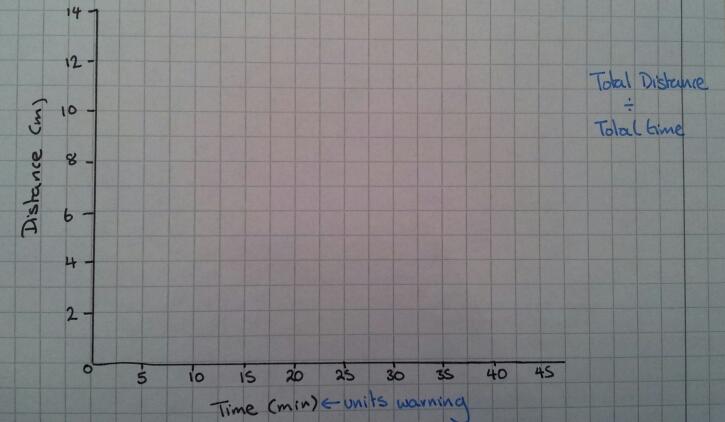
Idea 2
A speed-distance graph
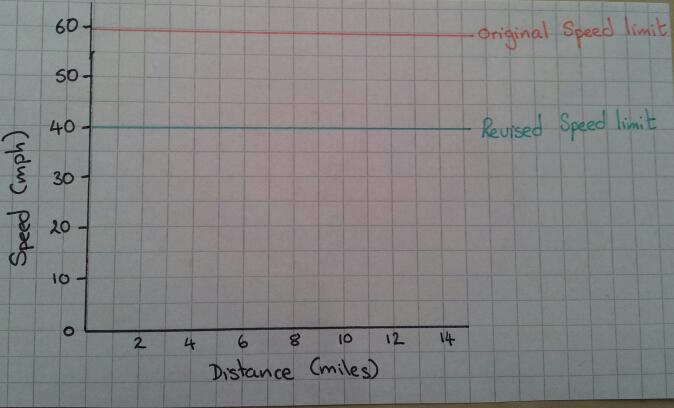
Idea 3
A speed-time graph
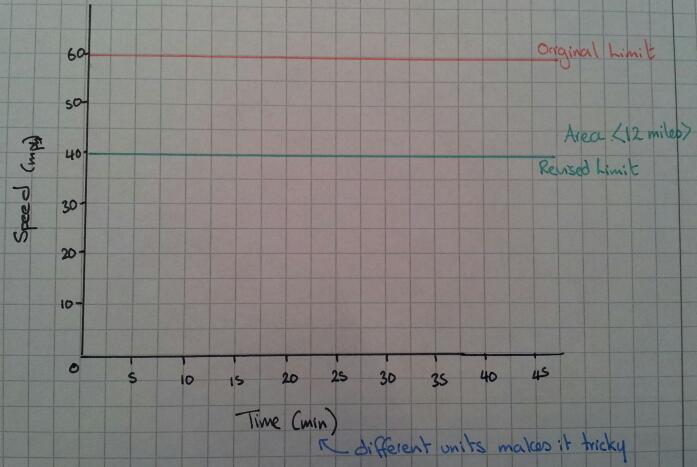
The straightforward option
How long should it take you to get through the roadworks if you stick to exactly 40mph? What does this look like on a graph? Which type of graph shows this information best?
Top Gear Alert
The boy racer wants to go fast, but avoid a ticket – what could he do?
Hint
What does ‘Average Speed’ actually mean?
Can you instantly jump between speeds?
Is acceleration going to effect your calculations?
What assumptions should you make about acceleration?
Do you need to work out the area under the graph or the gradient at all? How will you do this?
Can you describe what is going on?
Is it safe/legal?
Outcome
Your students should be able to produce many different graphs of how to stay on the right side of an average speed zone. They should be able discuss their findings with each other. However the morality or safety of their driving ideas may be a topic of discussion for a later PSE lesson …
Christmas has come early to my local Co-Op. I was intrigued enough to buy and eat the new Christmas chocolate, but not before marvelling at the mathematical elegance of it’s structure:
Image credit: http://www.distinctiveconfectionery.com/personalised-christmas-triangular-toblerone-box.html
The slab of equilateral chocolate breaks up into 9 smaller equilateral triangles. Or you could tessellate more of the big triangle.
Break off the corners and you get a hexagon.
Break off one corner and you get a trapezium.
Two triangles together makes a parallelogram … or it a rhombus? Good discussion point there!
The bar weighs 60g – how much does each triangle weigh? What about the weights of the other shapes you could make?
The dimensions are listed as 180x180x10mm. Where would these measurements fit on the triangle? Is it the length, width and height? Why? Can you calculate the dimensions of the other possible shapes?
Once you start thinking about it, there are lots of activities you could do … and there is the potential to eat your work! As usual, if you are going to do this, make sure you are aware of food allegeries.
I take no responsibility for this blog post. It is all down to the amazing teachers I work with. We have recently had our Year 6 open day and one of the activities was this amazing tessellation:
As you can see each rhombus has a pattern or picture which links to the next rhombus. You can stand in front of the full wall display and spend ages tracing the different routes across the wall. The clever use of colour means that from a distance the wall pops out as 3D cubes. Older students at school have commented that the display is ‘Awesome!’ and ‘Amazing!.
It was inspired by Vi Hart’s videos on snakes and doodling: YouTube
You know you are a Maths teacher when you go around a British city seeing shapes and maths everywhere AND you take pictures of it! Here are some discussion starters based around the area of Liverpool ONE:
Curved building
What would the plans and elevations look like? Why do you think the side windows are parallelograms not rectangles? Are the end windows similar shapes? What mathematical word describes distorting a shape? (Skew)
Stacked shapes
What would a plan and elevation of this building look like? What shape is the base of the projected level? (Trapezium)
Sine wave
Is this an approximation of a sine wave? Is it representing a convergent sequence?
Triangular roof
Why are triangles so popular in architecture?
Interesting shopfront projection
What would an aerial view look like? Would you see the zigzag projections?
Security door
What shapes can you see? Is it like isometric or squared dotty paper?
Curved stairwell
What mathematical things can you see? Are the handrails parallel?
Circular skylight
What features of a circle can you see?
If you like Takeaway homeworks or need a resource for the area and perimeter of circles, including some arc/sector challenges, then my third takeaway homework is for you!