A prescription says to take 2 pills every 4 hours, but don’t take more than 8 pills in 24hrs. There are 100 pills in a prescription.
If you start taking them on the 22nd March, when do you stop taking them? Assume you start taking them at midday and are in bed by 2230.
You can’t get a more real-life maths problem than that!
If you offer personal finance as a compulsory part of the curriculum, stop reading now.
‘Pay day loan’ companies have been the subject of several news stories over the last few months. Do they make money from those suffering from financial strife? Are the people who take them out too short-sighted to see the long term impact? Are they bad at Maths?
Personally, I don’t think there is a simple answer to any of it. That is the reason I’ve started including pay day loans when I do percentages with KS4 pupils.
Loan calculator
This idea arose when I was revising with older pupils who had the skills to work out percentages, but were struggling to apply them.
I showed them the loan calculator sliders on Wonga.
I asked the class to estimate how much different loans would cost for different numbers of days. They showed their answers on whiteboards. I then showed the actual amount owed and we discussed it.
The questions they came up with and how they justified their choices were brilliant.
Student Examples
If you are always £100 short at the end of the month and continually paid off the loan with interest, what would you owe after a year?
(They spotted that after each month you would need £100, plus an extra months interest etc)
What is the APR? What does APR mean?
(It was 4214% on the day we discussed it)
Why do you pay fees on a loan?
Are pay day loans a bad thing as a one off, emergency solution?
(They were split on their answer to this one)
Some of these questions wouldn’t be relevant in a GCSE, but they are life skills which will hopefully benefit them in the future.
By the way, they were ‘gobsmacked’ when they realised how much interest you pay back on a mortgage and what percentage of your wages go on monthly repayments!
Percentages are all to do with proportion, but this seems to escape the understanding of some. If you calculate 20% of £15, this is different to 20% of £25. The 20% is not a fixed quantity. How can you explain this to visual learners?
Visual Percentages/Proportion
Equipment
Pencil
Ruler
Paper – squared makes the task easier
Coloured pencils (optional)
Calculations
Find 20% of 15, 10 and 0.
Construction
Draw a 15cm line, mark 3cm along it.
Move down 5cm.
Draw a line, mark 2cm along it.
Join the ends of the lines with a ruler and indicate this with a cross.
This should be 10cm lower than the bottom line.
Repeat, joining the 3cm and 2cm points.
Shade in the smaller triangle.
Label the lines.
The Maths bit
The width of the triangle indicates the whole amount (100%).
The shaded width represents 20%.
The unshaded width represents 80% (Ask students if they know why).
The whole diagram represents 20% of any number from 0 to 15.
This can be adapted for any number and percent. It visually shows that as a number gets bigger the percent increases proportionally.
You can also use this to investigate fractions.
Note: This is for comparing widths. You can challenge your students to prove whether it is also true for the areas of the triangles.
A different way to look at data and probability is to introduce letter frequency analysis.
I set pupils the task of finding out the letter frequency data for the english language. Not much of a challenge for a bright student with the internet.
However …
I then gave them four A4 sheets of symbols to decode. Literally four pages of code, with no hints except they had to determine two literary works and authors from it. They had two weeks to solve it.
In hindsight, they described it as the best homework ever. I had parents contact me to see if they had solved it correctly – not to help their child, they were in competition to see who would get it first!
How to do it
Pick a text which is freely available on the internet – it saves typing out pages of text. I chose ‘Through the Looking Glass’ by Lewis Carroll – lots of interesting words!
I found a great website which gives you the Dancing man cipher amongst others. You paste in your text and select your substitution cipher. It then encodes your text for you. I chose the Dancing Man as it was the second literary work: The Adventure of the Dancing men (A Sherlock Holmes story)
I pasted this into Word and this formed the homework.
The interesting thing about this substitution cipher is that it has 52 symbols and no spaces. It is tricky to cheat as you would have to know the name of the cipher and the full cipher was not published in the book. There is more than one variation of the code as different people have tried to fill in the missing symbols.
Classics
This task ticks all the boxes for data processing, coding, independent study and literacy. In fact several pupils came back and said they had read Conan-Doyle’s classic work as a result of a maths task.
This idea came about after a Departmental INSET on teaching the C3 unit run by my HoD.
Students never believe you when you tell them they must understand this topic as it’s an essential skill for their exam. So get them to tell you what is important…
Before you start
You will need a different GCSE paper for each student (I used Foundation non-calc). It is possible to use one between two.
You will also need pens, scissors, glue & display paper in four colours.
Cut and label
Each student cuts out the individual questions and labels them with the month & year eg Jan 12.
Sort 1
Each student sorts their questions into Number, Algebra, Data, Shape.
Sort 2
Assign each area of study to one of the sheets of display paper. The students pile their Number questions onto the Number sheet etc.
Categorise
Split the class into four groups and give each group one area of study to look at. They must sort the questions into common themes eg BIDMAS, sequences, pictograms.
Review
Ask each group what they notice eg in most exams there is a question related to drawing/reading a bar-chart.
Display
Each group sticks the questions down and labels the common themes.
The class spotted all of the common themes and key skills, without me turning into a nag. As you can see from my wall display, we needed an extra sheet for number questions. The foundation GCSE paper has 40% number questions, which equates to 2/5 of the exam – our work was spot on. During the revision sessions I have referred to this wall display frequently. It has also been a talking point for other classes.
Update
Mark Greenaway (@suffolkmaths) has made an instructional to go with this idea. Go to his website www.suffolkmaths.co.uk and select ‘Exam Advice – Supporting powerpoint’ to see it.
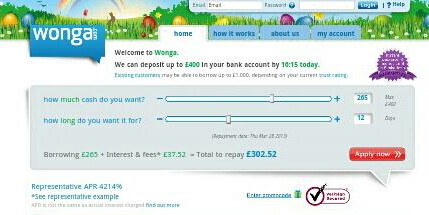
I was sat in a coffee shop when I overheard the barista say to a customer ‘Take your time, there are about 20,000 different drinks available’.
Sounded like a mathematical challenge to me.
If the menu below was real, how many different drinks could made?
How many would be drinkable?
Size: S, M, L
Drink: Filter, Americano, Cappucinno, Machiatto, Latte, Espresso, Hot chocolate.
Coffee type: Decaf or caffeinated
Flavour: Vanilla, Mint, Hazelnut, Ginger, Caramel, None
Milk: None, whole, skimmed, soya
Hint: Be methodical, work out the hot chocolate options first.
Solution
Hot choc
Size *Flavour*Milk = 3*6*4 = 72
Coffee
Size*Drink*Type*Flavour*Milk =
3*6*2*6*4 = 864
Total number of drinks
864 + 72 = 936
This doesn’t consider extra shots of coffee or syrup. Imagine how many variations there are in a big coffee shop!
Me … I’ll have a black filter, no milk, no sugar.
