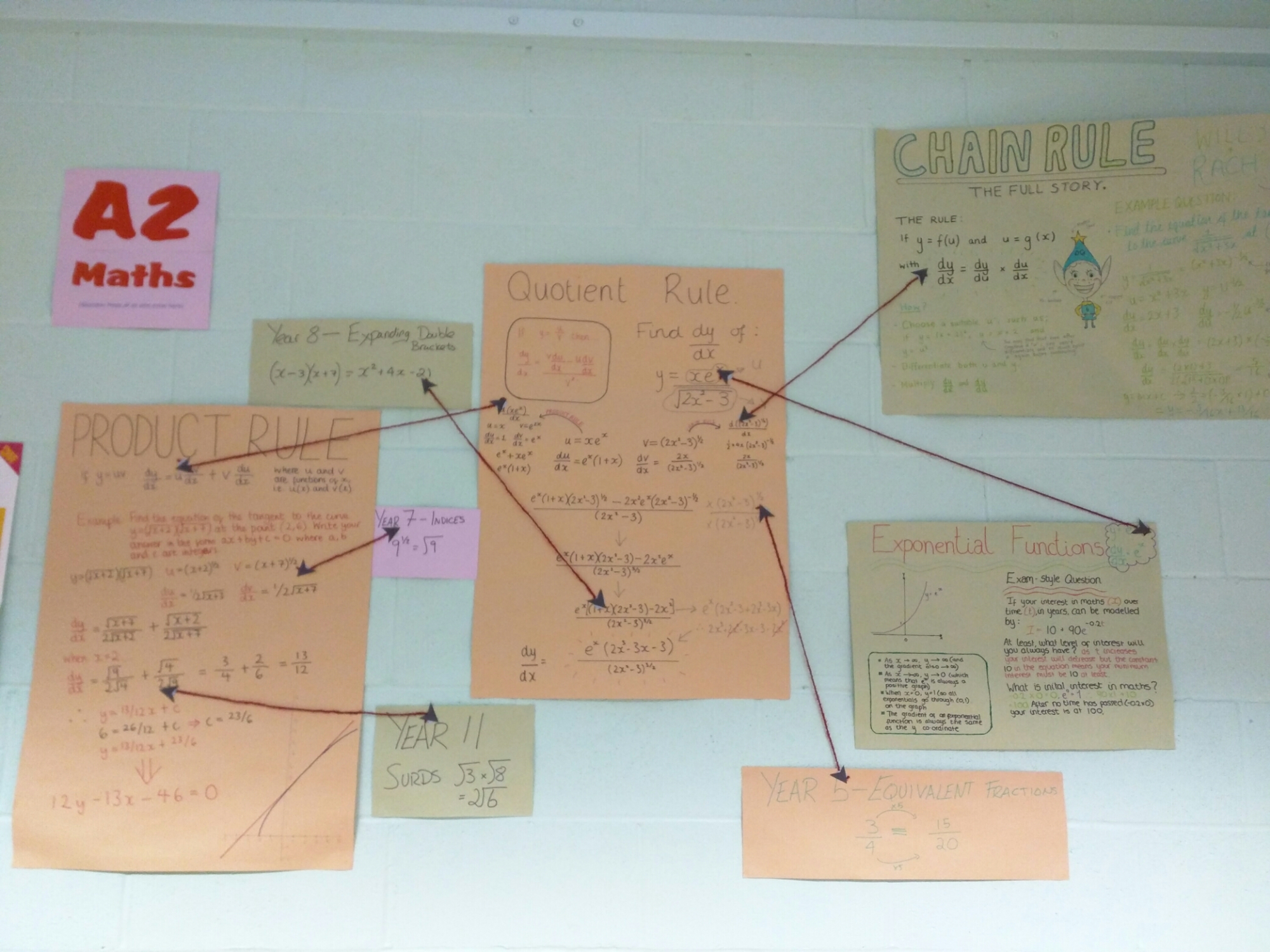
Oh, that question … heard often from the mouths of those who will not go on to study Maths at a higher level! But when it’s more able students who can’t see the necessity of fundamental principles … Well, that’s a bit worrying.
M’colleague, Mr D, has nailed the answer to this question. When I say ‘nailed’ I obviously mean ‘stuck’ and he has literally* stuck the answer on the wall.
*Note: Mathematician using correct definition of literally.
Here you go:
If you zoom in on this student work, on A2 Differentiation, you can see that he has annotated all the skills used and when you first meet them in the curriculum:
Such a simple idea to tie together seemingly unrelated parts of the Maths curriculum. It also reinforces the need to keep all basic skills sharp.
I’d say it was genius, but then I’d never hear the end of it!