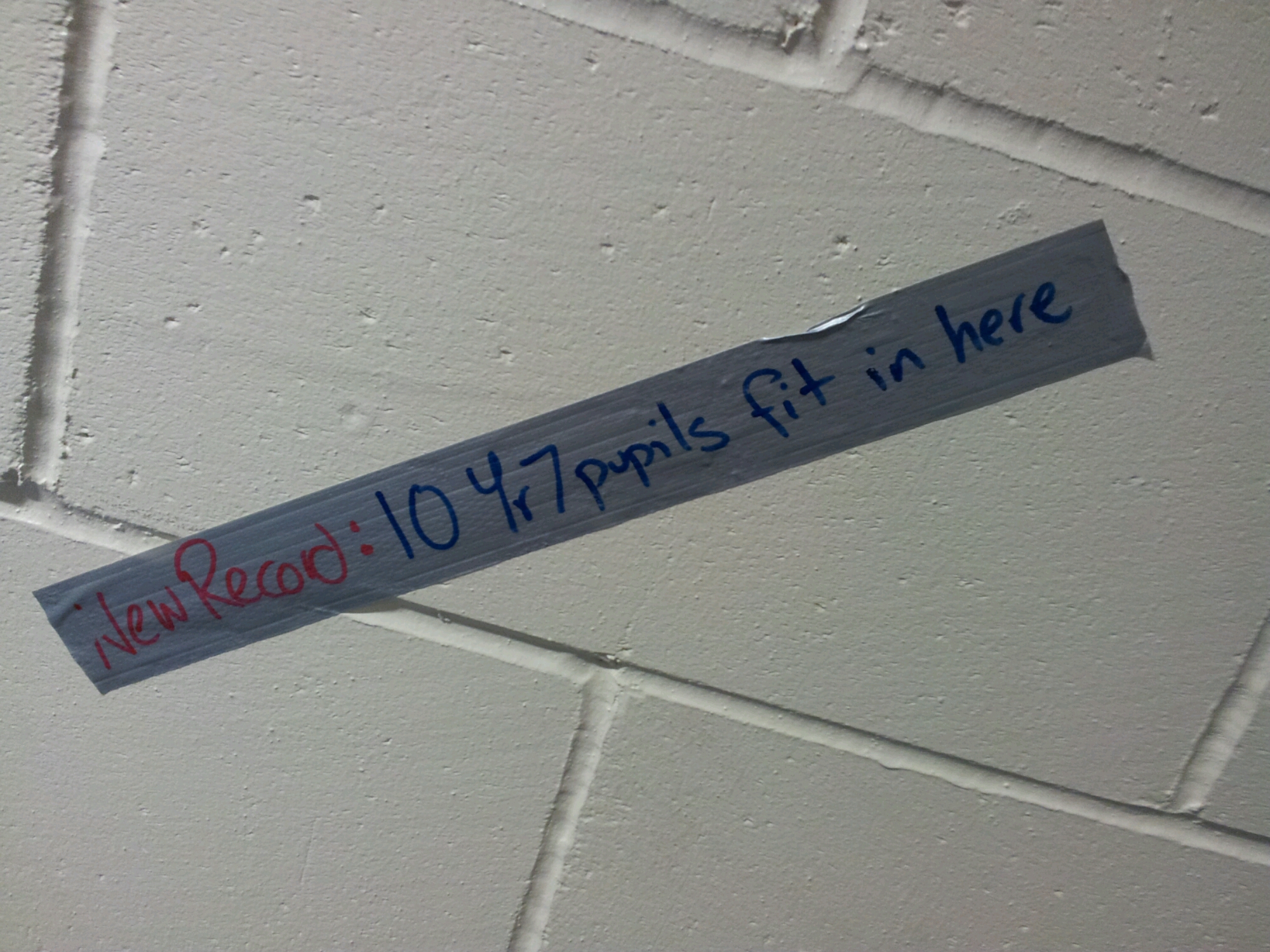Author Archives: MsKMP

234. (Students) cubed

1 Reply

Here is a quick fun starter to get your class thinking about dimensions and volume.

Question: How many students can you fit into a metre cube?

The discussion will probably include:

  • ‘How big is a metre?’ (find a metre stick)
  • ‘Did you mean standing in a square?’ (no)
  • ‘How big is the student?’ (average – that answer annoys students)
  • And finally ‘Huh?’ (ask the person next to you to explain)

Whilst this is going on make a metre square on the wall and the floor, using duct tape. The inner measurements of the cube are 1m, the rest is just tape border.

image

The Predictions
Draw up a quick tally chart of how many students they think will fit. A bright child will usually ask how are you going to find out. Easy …

Put students in the cube
Let them put themselves into the confines of the cube. Cue bouncy boys squashing up. Then remind them it can’t be higher than a metre. You might find it useful to have two spare students hold metre sticks vertically at the non-wall end to define the end of the cube.

We managed nine boys, plus gaps at the top for bits of a tenth boy – it wasn’t ethical to chop one up and sprinkle the bits. So we imagined the tenth person balanced on the gaps around their shoulders.

Ten? That is a new record for this activity!

image

The Point

  • Volume is the space inside a 3D shape.
  • One metre cube is bigger than you think.
  • It’s a memorable activity to refer back to.

Even better if …

I’d love to get sturdy board covered in birthday (or Christmas) paper to put under and around the cube to start a discussion about surface area. You could make a big show of unfolding the cube and laying the wrapping out on the floor to form a huge net.

 

Note
I used to do this by taping metre sticks into a cube, but they fell apart easily. In some schools three metre sticks is a challenge, twelve would be a miracle find. Duct tape works much better!

233. Summary Statistics

Leave a reply

If you are reading this blog there is a high probability that you are a maths teacher – it is a maths education blog after all. That means data shouldn’t be scary … should it?

scary data

Image credit: http://mrcbaker.blogspot.co.uk/2013/08/data-doesnt-have-to-be-scary-how-you.html (This website is worth a look!)

In a world of performance tracking and data analysis, seeing the trends in class data should be easy. However busy lives and hectic timetables mean we often don’t get the time to step back and reflect on our classes.

I decided to pull together the summary data for each of my classes onto one page. I can see a profile of current and target grades (FFTD*), gender, SEN and Ever6** information in one table. The actual act of completing the table made me take a closer look at the abilities and issues within the class. I realise not everyone uses these data measures so the files are in .doc and .docx form. Since the data is summarised it remains relatively anonymous, making it a good discussion document for trainee teachers or CPD.

You can download a customisable form here:
Summary Data for class KS3 (doc)
Summary Data for class KS3 (docx)
Summary Data for class KS4 (doc)
Summary Data for class KS4 (docx)
Summary Data for class KS4 sample (doc)
Summary Data for class KS4 sample (docx)

*FFTD means Fischer Family Trust Data

**Ever6 is a UK measure related to eligibility for Pupil Premium funding (simplified description).

233. Stealthy Cone Investigation

Leave a reply

I like to encourage students to discover rules and formulae for themselves. It’s important that students understand where the maths comes from so they can apply their skills effectively. They also don’t have to rely on remembering a rule (which they may forget when they are stressed).

net of a cone

Image credit: http://www.ck12.org/geometry/Surface-Area-and-Volume-of-Cones/

This resource is a neat and effective way to investigate the surface area of a cone through measuring circles and creating a 3D shape. Students get a physical feel for how the dimensions fit together. Throughout the lesson I let students choose their degree of accuracy in cutting, measuring and calculating. Of course, when we discussed the ‘solution’ at the end of the session it was impossible for me to put one correct answer on the board. So I generalised using a and b for the radii – explaining that everyone could check their method in general terms. The lovely ‘penny drop’ moment happened when my a’s and b’s suddenly became a general rule. I’d conned the class into using algebra because of the accuracy issue.

Download the worksheet and answers here: Surface_area_of_a_cone

Hint: Copying onto coloured paper or card makes this activity stand out in their notes.

232. Steps in Volume

2 Replies

This is a quick little post to give you a nifty little resource inspired by the ideas of Bruno Reddy (@MrReddyMaths). I suggest you visit his website at: http://mrreddy.com/.

Sphere cone pyramid

Image Credit: http://k12math.com/math-concepts/algebra/volumes/volumes.htm

I’ve been teaching my class how to calculate the volume of spheres, cones and pyramids. They really like these staged worksheets. You could print them out as they are, but I personally print them as A5 booklets which fit into their books.

Volume of Sphere Cone Cylinder (pdf)

231. Fish Shop Maths

7 Replies

I’ve been using this idea since I first started teaching and I’ve finally got around to typing it up!

fish_chips

Image Credit:http://coachandhorsesn16.com/eat/fish-n-chips/

I introduce order of operations by creating an imaginary Chip Shop. I usually read out orders and get the students to write down what they think they are on whiteboards. Note that when you read out the orders, the punctuation doesn’t give any hints.

  • ‘Two fish and three chips’ – 2 fish & 3 portions of chips
  • ‘Fish and chips twice’ – 2 fish & 2 portions of chips or 1 fish & 2 portions of chips
  • ‘Five sausage and chips’ – 5 sausages & 5 portions of chips or 5 sausages & 1 portion of chips

This activity always prompts a ‘discussion’ as to who is correct. The misconception of what an order could mean links nicely with the misconception when working out 2 + 3 x 4. You could also adapt the idea for writing algebraic expressions.

A presentation, with questions, is downloadable in three different formats here:

Fish Shop BIDMAS (pptx)

Fish Shop BIDMAS (ppt)

Fish Shop BIDMAS (ppsx)

 

 

230. Resource of the week

Leave a reply

I came across this splendid resource on Similar Triangles, by cturner16, on the TES website:
Similar triangles matching activity

The cards start with a standard diagram of overlapping triangles and you match it up with the individual triangles. The final step is to work out the scale factor and the missing side. It follows the exact steps you would want students to follow when working on these problems.

Now, I know my class well and to avoid the standard bickering, mess and ‘I didn’t think you meant pick up every sheet when you said pick up every sheet’, I copied every set on a different colour:

image

The colour made it so much easier to manage and discuss. There are six problems, so if your students work in 2’s or 3’s, they each get 3 or 2 sets to stick in their book. The problems are full of misconceptions and interesting scale factors. I’m really glad I used it!

Thank you cturner16!

229. Speed Camera Maths

1 Reply

Speed Cameras are so last century: discerning law enforcement agencies favour the Average Speed Camera!

image

These motorway delights timestamp when you go through certain checkpoints and calculate your speed between them. No complicated laser guns required, just number plate recognition and a little distance/time calculation. This already sounds like a KS3/4 class activity or a Mechanics A-Level starter.

Equipment
Squared paper
Pencil
Ruler
Coloured pens
Calculator (optional)

Question
Can you find three different (safe) strategies for staying on the right side of the law through extended roadworks? You must average 40mph over 12 miles (original speed limit 60mph).

Visual Prompt
To start off with just draw out blank axes and discuss how you could visually represent this problem.

Idea 1
A distance-time graph

image

Idea 2
A speed-distance graph

image

Idea 3
A speed-time graph

image

The straightforward option
How long should it take you to get through the roadworks if you stick to exactly 40mph? What does this look like on a graph? Which type of graph shows this information best?

Top Gear Alert
The boy racer wants to go fast, but avoid a ticket – what could he do?

Hint
What does ‘Average Speed’ actually mean?
Can you instantly jump between speeds?
Is acceleration going to effect your calculations?
What assumptions should you make about acceleration?
Do you need to work out the area under the graph or the gradient at all? How will you do this?
Can you describe what is going on?
Is it safe/legal?

Outcome
Your students should be able to produce many different graphs of how to stay on the right side of an average speed zone. They should be able discuss their findings with each other. However the morality or safety of their driving ideas may be a topic of discussion for a later PSE lesson …